Solve the differential equation (x^4 - 2x^2y^2 + y^4) dx - (2x^2y - 4xy^3 + sin y) dy = 0.
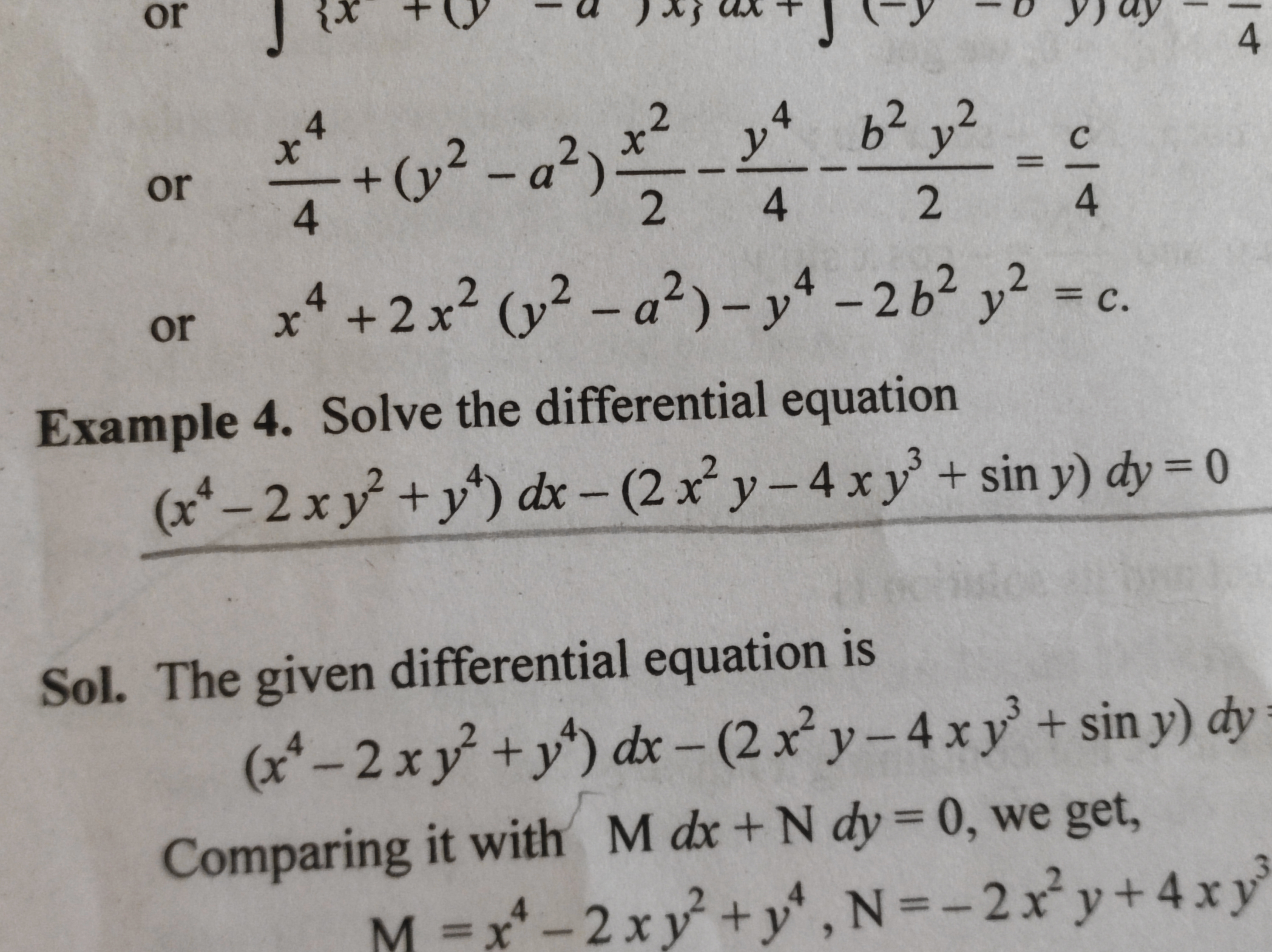
Understand the Problem
The question is asking to solve a specific differential equation given in the problem statement. This involves applying appropriate mathematical techniques to find a solution to the equation.
Answer
The solution is given by the implicit function \( F(x, y) = C \), where \( F \) is determined from the integrated parts of \( M \) and \( N \).
Answer for screen readers
The solution to the differential equation is given implicitly by the equation
$$ F(x, y) = C $$
where ( F ) is derived from the integrated terms of ( M ) and ( N ).
Steps to Solve
- Identify the Differential Equation The equation given is
$$(x^4 - 2x^2y^2 + y^4) dx - (2x^2y - 4xy^3 + \sin y) dy = 0.$$
Let ( M = x^4 - 2x^2y^2 + y^4 ) and ( N = - (2x^2y - 4xy^3 + \sin y) ).
- Check for Exactness To check if the differential equation is exact, calculate
$$ \frac{\partial M}{\partial y} \quad \text{and} \quad \frac{\partial N}{\partial x}. $$
We compute:
- ( M_y = \frac{\partial}{\partial y}(x^4 - 2x^2y^2 + y^4) = -4x^2y + 4y^3 )
- ( N_x = \frac{\partial}{\partial x}(- (2x^2y - 4xy^3 + \sin y)) = -4xy + 2y )
- Solve for Exactness If ( \frac{\partial M}{\partial y} ) equals ( \frac{\partial N}{\partial x} ), the equation is exact.
This gives us:
- ( M_y = -4x^2y + 4y^3 )
- ( N_x = -4xy + 2y )
Check if: $$ -4x^2y + 4y^3 \neq -4xy + 2y $$
So the equation is not exact.
- Find an Integrating Factor Since the equation is not exact, we need to find an integrating factor. A common integrating factor can often be a function of ( x ) or ( y ). Assuming a function of ( y ), we calculate:
$$ \mu(y) = \frac{1}{N_y - M_x}. $$
- Solve for the Integrating Factor Calculate ( N_y ) and ( M_x ):
- ( N_y = -2x^2 + 12xy^2 + \cos y )
- ( M_x = 4x^3 - 4xy^2 $$
Assuming ( \mu(y) = \cos y ), we can multiply through the original equation to find a new, exact equation.
- Integrate to Find the Solution After finding the new exact equation, we integrate ( M ) and ( N ) with respect to ( y ) and ( x ) respectively to find the potential function ( F(x,y) = C ).
The solution to the differential equation is given implicitly by the equation
$$ F(x, y) = C $$
where ( F ) is derived from the integrated terms of ( M ) and ( N ).
More Information
This differential equation involves non-linear terms and requires finding an integrating factor to make it exact. Understanding exact equations and integrating factors is fundamental to solving many differential equations.
Tips
- Failing to verify if the equation is exact before proceeding.
- Not simplifying the terms correctly when calculating the partial derivatives.
- Assuming a wrong form for the integrating factor without showing the calculations.