Solve the differential equation \( \frac{dp}{dt} = t^2 p - p + t^2 - 1. \)
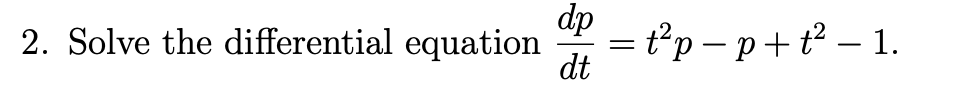
Understand the Problem
The question is asking to solve a differential equation provided in the form of a first-order equation involving the variable p and the function of t. We will analyze the equation to find a suitable method for solving it, such as separation of variables or integrating factors.
Answer
The solution to the differential equation is $$ p = k e^{\frac{t^3}{3} - t} - 1 $$ where \( k \) is a constant.
Answer for screen readers
The solution to the differential equation is
$$ p = k e^{\frac{t^3}{3} - t} - 1 $$
where ( k ) is a constant determined by initial conditions.
Steps to Solve
- Rewrite the equation
Start with the given differential equation:
$$ \frac{dp}{dt} = t^2 p - p + t^2 - 1 $$
This can be rewritten as:
$$ \frac{dp}{dt} = p(t^2 - 1) + (t^2 - 1) $$
- Factor the right-hand side
Factor out the common term $(t^2 - 1)$:
$$ \frac{dp}{dt} = (t^2 - 1)(p + 1) $$
- Separate variables
Separate the variables ( p ) and ( t ):
$$ \frac{1}{p + 1} dp = (t^2 - 1) dt $$
- Integrate both sides
Integrate both sides:
$$ \int \frac{1}{p + 1} dp = \int (t^2 - 1) dt $$
This gives:
$$ \ln |p + 1| = \frac{t^3}{3} - t + C $$
where ( C ) is the constant of integration.
- Solve for ( p )
Exponentiate both sides to solve for ( p ):
$$ |p + 1| = e^{\frac{t^3}{3} - t + C} $$
Let ( k = e^{C} ):
$$ p + 1 = k e^{\frac{t^3}{3} - t} $$
Therefore,
$$ p = k e^{\frac{t^3}{3} - t} - 1 $$
The solution to the differential equation is
$$ p = k e^{\frac{t^3}{3} - t} - 1 $$
where ( k ) is a constant determined by initial conditions.
More Information
This type of differential equation is a first-order separable equation. The solution includes an exponential term, which often appears in the solutions of such equations. The constant ( k ) allows for different particular solutions depending on initial or boundary conditions provided.
Tips
- Not properly separating variables: Make sure to move all ( p ) terms to one side and ( t ) terms to the other side.
- Forgetting constant integration: Always add the constant of integration ( C ) after integrating.
- Incorrectly solving for ( p ): Watch out for sign mistakes when isolating ( p ).
AI-generated content may contain errors. Please verify critical information