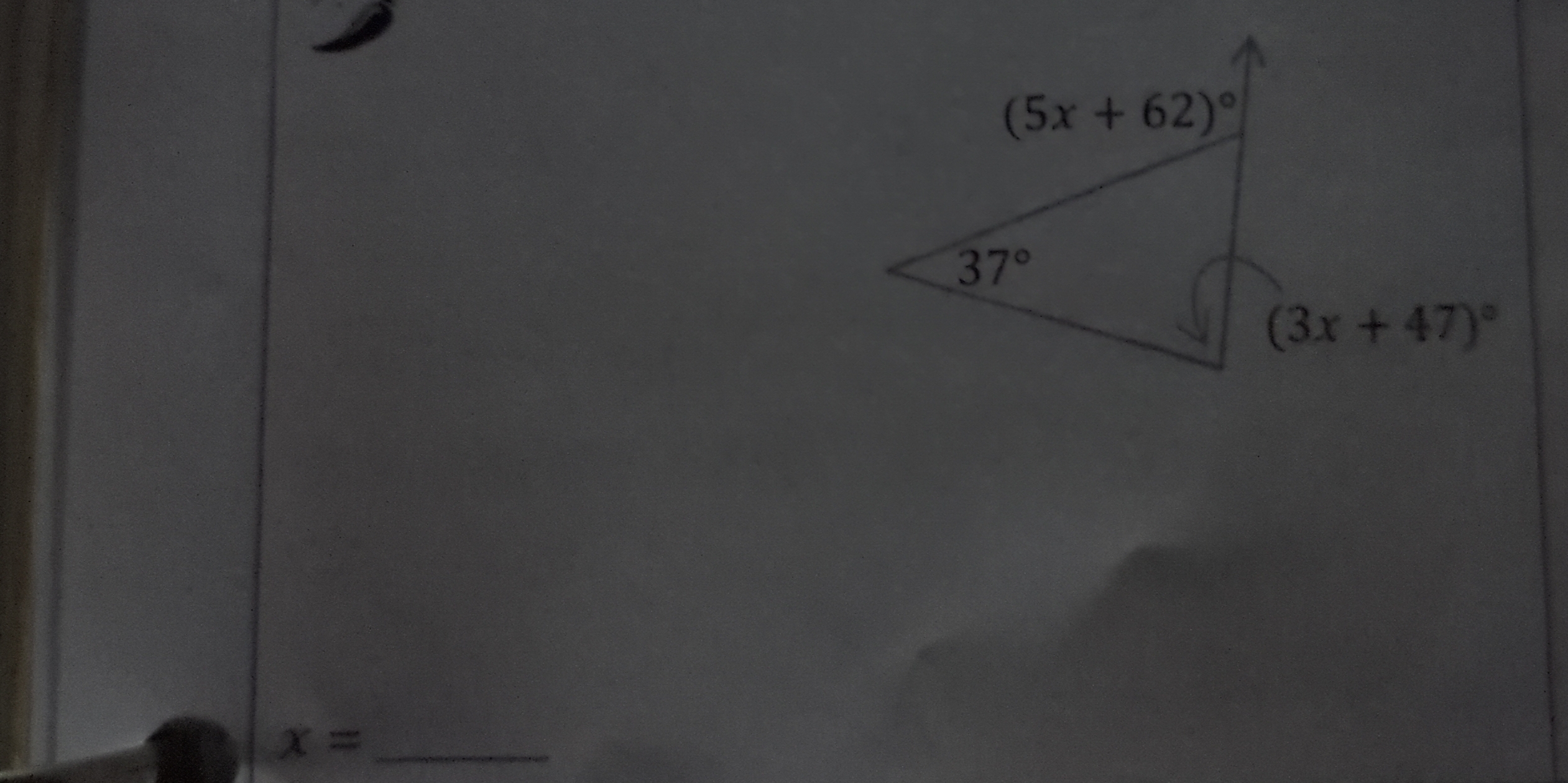
Solve for x in the triangle with angles (5x + 62)°, 37°, and (3x + 47)°.

Understand the Problem

The question is asking to solve for the variable x using the angles present in a triangle, which are expressed in terms of x. The angles given are (5x + 62)°, 37°, and (3x + 47)°, and they must sum to 180° since the sum of angles in a triangle is always 180°.

Answer

$x = 4.25$

Steps to Solve

Write the equation based on angle sum property
Since the sum of the angles in a triangle must equal 180°, we can set up the equation:
$$(5x + 62) + 37 + (3x + 47) = 180$$
Combine like terms
Combine the constant terms and the terms with $x$:
$$5x + 3x + 62 + 37 + 47 = 180$$
This simplifies to:
$$8x + 146 = 180$$
Isolate the variable $x$
Subtract 146 from both sides to isolate the term with $x$:
$$8x = 180 - 146$$
This results in:
$$8x = 34$$
Solve for $x$
Now, divide both sides by 8:
$$x = \frac{34}{8} = 4.25$$

$x = 4.25$

More Information

The value of $x$ allows us to find the individual angles of the triangle. By substituting $x = 4.25$ back into the expressions for the angles, the angles will be calculated as follows:

First angle: $5(4.25) + 62 = 21.25 + 62 = 83.25°$
Second angle: $37°$
Third angle: $3(4.25) + 47 = 12.75 + 47 = 59.75°$
These angles satisfy the triangle angle sum property: $83.25° + 37° + 59.75° = 180°$.

Tips

Ignoring angle sum property: Failing to set the equation based on the property that the sum of angles in a triangle equals 180°.
Arithmetic errors: Mistakes in adding or subtracting the constants when combining like terms.
Division errors: Incorrectly dividing or miscalculating when isolating $x$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!