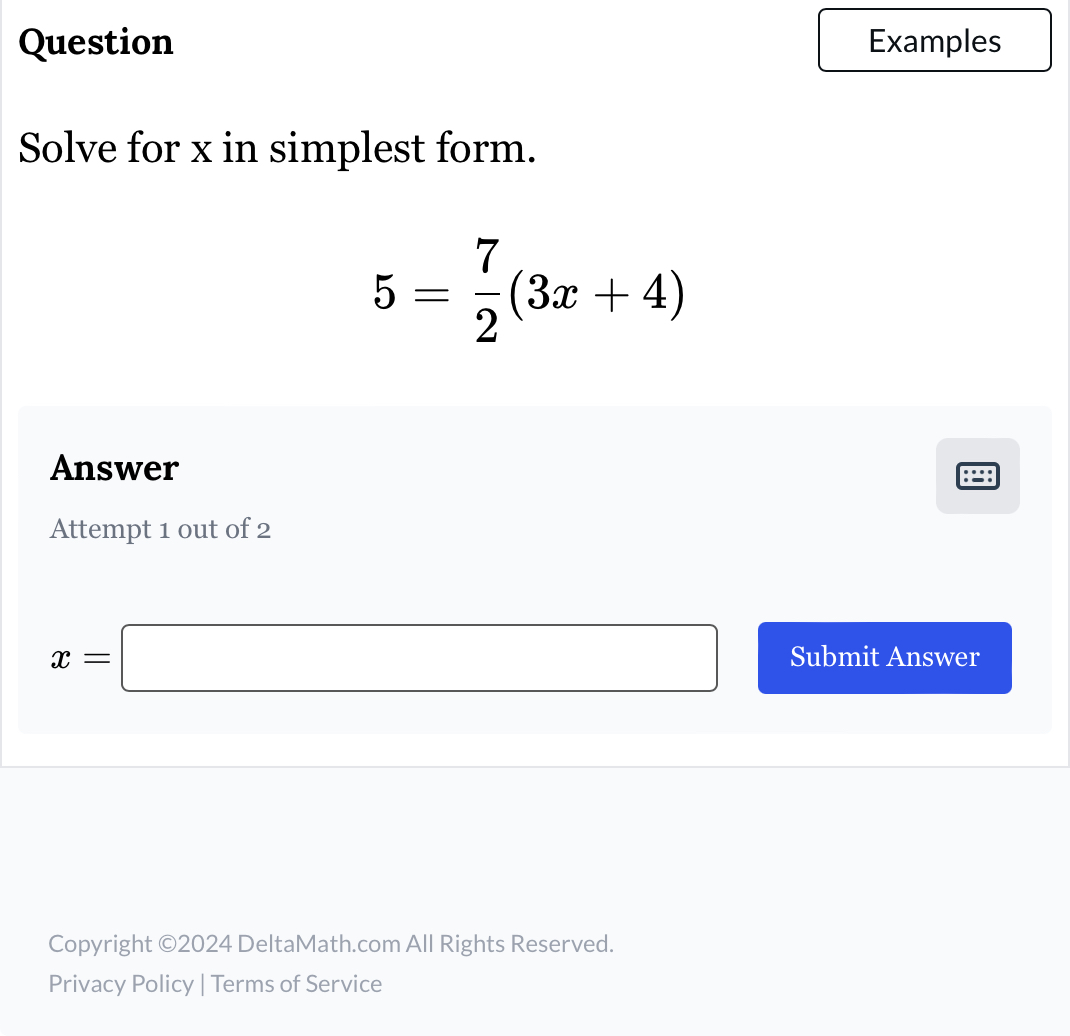
Solve for x in simplest form. 5 = (7/2)(3x + 4)
Understand the Problem
The question is asking to solve the equation for x, specifically defined by the expression given on the left side of the equation equal to a fraction applied to a linear expression involving x. The goal is to find the value of x in its simplest form.
Answer
$$ x = \frac{-6}{7} $$
Answer for screen readers
$$ x = \frac{-6}{7} $$
Steps to Solve
-
Set up the equation
The equation to solve is given as:
$$ 5 = \frac{7}{2}(3x + 4) $$ -
Eliminate the fraction
Multiply both sides of the equation by 2 to eliminate the fraction:
$$ 2 \cdot 5 = 7(3x + 4) $$
This simplifies to:
$$ 10 = 7(3x + 4) $$ -
Distribute the 7
Distribute the 7 on the right side of the equation:
$$ 10 = 21x + 28 $$ -
Isolate the variable term
Subtract 28 from both sides:
$$ 10 - 28 = 21x $$
This simplifies to:
$$ -18 = 21x $$ -
Solve for x
Divide both sides by 21:
$$ x = \frac{-18}{21} $$
Now simplify the fraction:
$$ x = \frac{-6}{7} $$
$$ x = \frac{-6}{7} $$
More Information
The value of ( x ) is negative because the initial equation sets up a scenario where ( 5 ) is less than ( 7(3x + 4) ). The process of solving involved eliminating fractions, distributing, and isolating the variable, which are common steps in algebra.
Tips
- Forgetting to distribute correctly when applying multiplication.
- Neglecting to simplify fractions after finding ( x ).
- Making arithmetic errors when combining or subtracting terms.
AI-generated content may contain errors. Please verify critical information