Solve for x and y given the parallelogram.
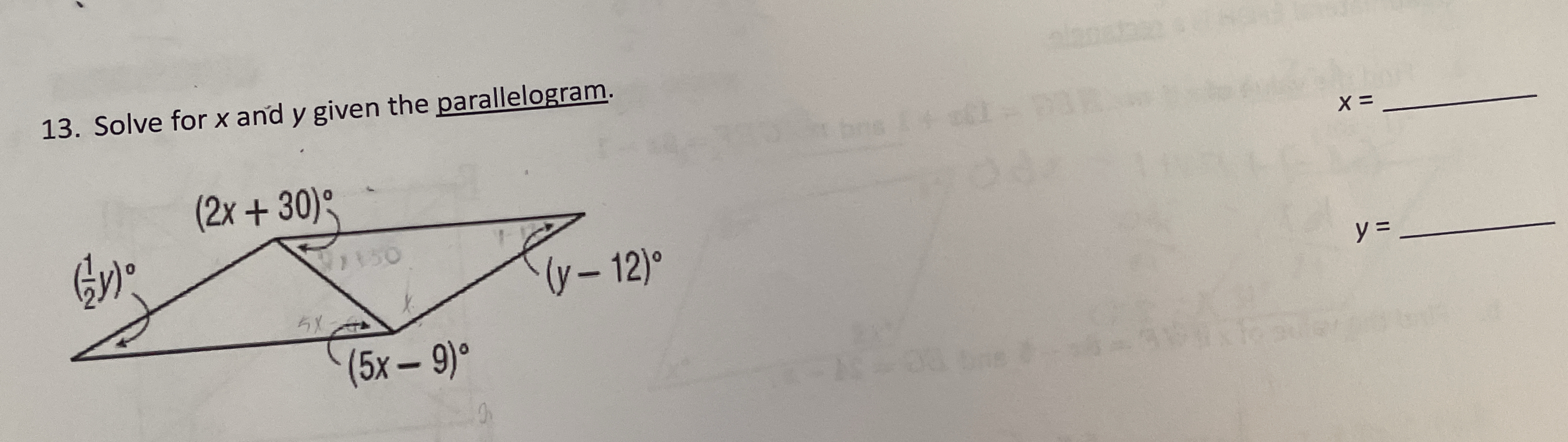
Understand the Problem
The question is asking to solve for the values of x and y in the context of a given parallelogram, which involves using the properties of the angles in the shape.
Answer
$x \approx 22.71$, $y = 128$
Answer for screen readers
$x \approx 22.71$
$y = 128$
Steps to Solve
- Identify angle relationships in the parallelogram
In a parallelogram, opposite angles are equal, and consecutive angles are supplementary (add up to 180°). Here, we can establish two equations based on the given angles.
- Set up the first equation using consecutive angles
The angle represented as $(2x + 30)^\circ$ and the angle represented as $(5x - 9)^\circ$ are consecutive angles.
The relationship can be expressed as:
$$(2x + 30) + (5x - 9) = 180$$
- Simplify and solve for x
Combine like terms in the equation and isolate (x):
$$2x + 30 + 5x - 9 = 180$$
$$7x + 21 = 180$$
$$7x = 180 - 21$$
$$7x = 159$$
$$x = \frac{159}{7}$$
$$x = 22.71$$ (approximately)
- Set up the second equation using the other angles
The angle represented as $\left(\frac{1}{2}y\right)^\circ$ and the angle represented as $(y - 12)^\circ$ are also consecutive angles.
The relationship can be expressed as:
$$\frac{1}{2}y + (y - 12) = 180$$
- Simplify and solve for y
Combine like terms in the equation and isolate (y):
$$\frac{1}{2}y + y - 12 = 180$$
$$\frac{3}{2}y - 12 = 180$$
$$\frac{3}{2}y = 180 + 12$$
$$\frac{3}{2}y = 192$$
$$y = \frac{192 \cdot 2}{3}$$
$$y = \frac{384}{3}$$
$$y = 128$$
$x \approx 22.71$
$y = 128$
More Information
In a parallelogram, the properties of angles lead to the establishment of systems of equations. Here, the relationships exploited allowed us to find the values of both (x) and (y).
Tips
- Not recognizing that consecutive angles are supplementary: Always remember that in parallelograms, adjacent angles add to 180°.
- Confusing the relationships of opposite angles: Ensure you understand that opposite angles in a parallelogram are equal.
AI-generated content may contain errors. Please verify critical information