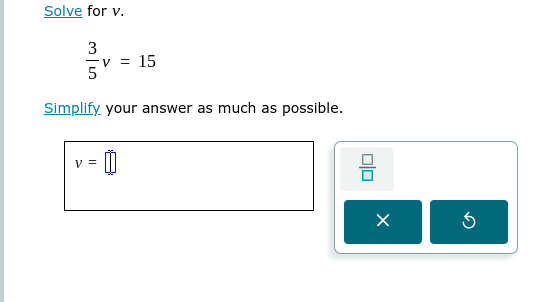
Solve for v in the equation (3/5)v = 15. Simplify your answer as much as possible.

Understand the Problem

The question is asking us to solve the equation (3/5)v = 15 for the variable v and simplify the answer as much as possible.

Answer

The value of \( v \) is \( 25 \).

Steps to Solve

Multiply both sides by the reciprocal To isolate ( v ), we first need to eliminate the fraction. We can do this by multiplying both sides of the equation by the reciprocal of ( \frac{3}{5} ), which is ( \frac{5}{3} ).

[ \frac{5}{3} \cdot \left( \frac{3}{5} v \right) = \frac{5}{3} \cdot 15 ]

Simplify the left side When we multiply ( \frac{5}{3} ) by ( \frac{3}{5} v ), the ( \frac{3}{5} ) and ( \frac{5}{3} ) cancel each other out:

[ v = \frac{5}{3} \cdot 15 ]

Calculate the right side Next, we simplify ( \frac{5}{3} \cdot 15 ):

[ v = \frac{5 \cdot 15}{3} ]

Perform the multiplication and division Calculate the product in the numerator:

[ v = \frac{75}{3} ]

Final simplification Now, divide ( 75 ) by ( 3 ):

[ v = 25 ]

The value of ( v ) is ( 25 ).

More Information

The equation used here is a straightforward application of isolating a variable by multiplying both sides by the reciprocal of the coefficient of that variable. This method can be broadly applied in algebra to solve equations involving fractions.

Tips

Not multiplying both sides by the same number: Always ensure to keep the equation balanced by performing the same operation on both sides.
Miscalculating the multiplication: Double-check basic multiplication and division steps to avoid arithmetic errors.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!