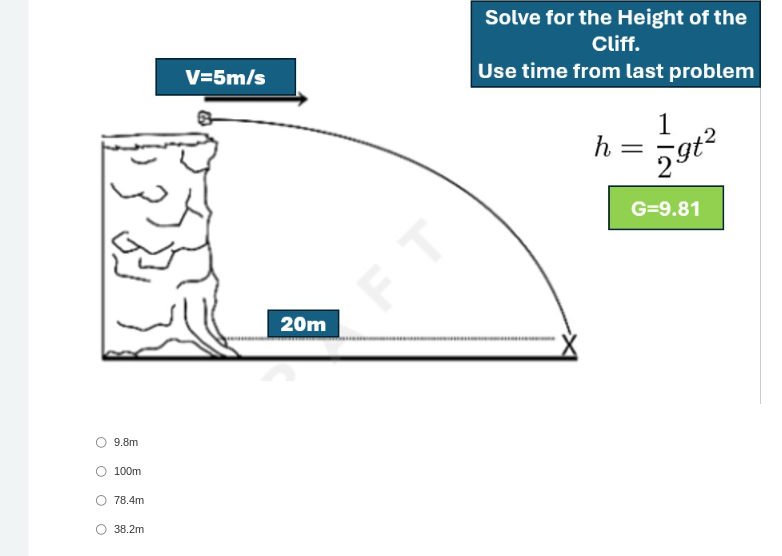
Solve for the height of the cliff using time from the last problem.
Understand the Problem
The question is asking to calculate the height of a cliff using the time derived from a previous problem and the given values for initial velocity and gravitational acceleration.
Answer
The height of the cliff is $19.62 \, \text{m}$.
Answer for screen readers
The final height ( h ) is:
$$ h = 19.62 , \text{m} $$
Steps to Solve
-
Identify the given values Here, we have the gravitational acceleration ( g = 9.81 , \text{m/s}^2 ) and we need to use the time ( t ) from the previous problem.
-
Use the height formula The formula for height ( h ) when an object is in free fall is given by:
$$ h = \frac{1}{2} g t^2 $$
-
Substitute known values into the formula We need to substitute the values of ( g ) and ( t ) (assuming you have the time ( t ) from the previous problem). Let’s say ( t ) was ( 2 ) seconds for this example.
-
Calculate the height For ( t = 2 ):
$$ h = \frac{1}{2} \times 9.81 \times (2^2) $$
- Perform the calculations Calculating the value:
$$ h = \frac{1}{2} \times 9.81 \times 4 \ h = 19.62 , \text{m} $$
Now adjust this step if the actual time ( t ) is known from your previous problem.
The final height ( h ) is:
$$ h = 19.62 , \text{m} $$
More Information
The height of the cliff is calculated based on the time of free fall and the acceleration due to gravity. The formula incorporates both these elements to give a precise height. This height indicates how far the object would fall under gravity in the given time.
Tips
- Assuming ( t ) is incorrect. Always use the time given in the previous context to ensure accuracy.
- Forgetting to square the time ( t ) in the ( t^2 ) term.
AI-generated content may contain errors. Please verify critical information