Solve for f: 5 - 2/f + 3/2f = f - 1/2f + 4.
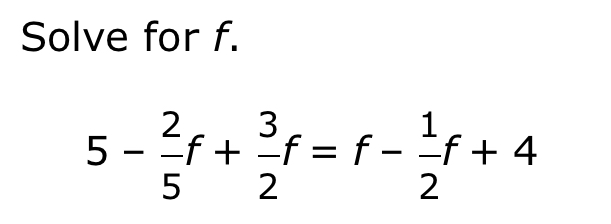
Understand the Problem
The question is asking to solve the equation for the variable f. It presents an algebraic equation that needs manipulation and simplification to isolate f on one side of the equation.
Answer
$$ f = -\frac{5}{3} $$
Answer for screen readers
The final answer is: $$ f = -\frac{5}{3} $$
Steps to Solve
- Combine like terms on the left side
Start by simplifying the left side of the equation: $$ 5 - \frac{2}{5}f + \frac{3}{2}f $$
Convert $ \frac{2}{5}f $ and $ \frac{3}{2}f $ to a common denominator. The least common multiple of 5 and 2 is 10. Thus: $$ \frac{2}{5}f = \frac{4}{10}f $$ $$ \frac{3}{2}f = \frac{15}{10}f $$
Now substitute: $$ 5 - \frac{4}{10}f + \frac{15}{10}f $$
Combine the like terms: $$ 5 + \frac{15 - 4}{10}f = 5 + \frac{11}{10}f $$
- Simplify the right side
Now simplify the right side of the equation: $$ f - \frac{1}{2}f + 4 $$
Convert $ \frac{1}{2}f $ to a common denominator of 2: $$ f - \frac{1}{2}f = \frac{2}{2}f - \frac{1}{2}f = \frac{1}{2}f $$
Substituting this back results in: $$ \frac{1}{2}f + 4 $$
- Set the simplified sides equal to each other
Now equate the simplified left and right sides: $$ 5 + \frac{11}{10}f = \frac{1}{2}f + 4 $$
- Isolate f on one side
To isolate $f$, first subtract $4$ from both sides: $$ 1 + \frac{11}{10}f = \frac{1}{2}f $$
Next, subtract $\frac{1}{2}f$ from both sides: $$ 1 + \frac{11}{10}f - \frac{5}{10}f = 0 $$
Combine like terms: $$ 1 + \frac{6}{10}f = 0 $$
- Solve for f
Now, subtract 1 from both sides: $$ \frac{6}{10}f = -1 $$
Multiply both sides by the reciprocal of $\frac{6}{10}$: $$ f = -1 \cdot \frac{10}{6} $$
This simplifies to: $$ f = -\frac{10}{6} = -\frac{5}{3} $$
The final answer is: $$ f = -\frac{5}{3} $$
More Information
This solution shows how to manipulate algebraic equations by combining like terms, finding common denominators, and isolating the variable. The final result indicates the value of $f$ that satisfies the original equation.
Tips
One common mistake is ignoring the need for a common denominator when combining fractions. It's vital to ensure all fractional coefficients are in the same terms before adding or subtracting them.
AI-generated content may contain errors. Please verify critical information