sin(π/2 - x) cot(π/2 + x) = -sin x
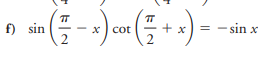
Understand the Problem
The question is asking to simplify or solve the equation involving trigonometric functions: sin(π/2 - x) * cot(π/2 + x) = -sin x.
Answer
The equation is valid for all values of $x$ where defined.
Answer for screen readers
The equation is valid for all values of $x$ where the functions are defined.
Steps to Solve
- Apply Trigonometric Identities
Using the co-function identities:
- $\sin(\frac{\pi}{2} - x) = \cos(x)$
- $\cot(\frac{\pi}{2} + x) = -\tan(x)$
Thus, we can rewrite the equation:
$$ \sin\left(\frac{\pi}{2} - x\right) \cot\left(\frac{\pi}{2} + x\right) = \cos(x) \cdot (-\tan(x)) $$
- Simplify Further
The tangent function can be expressed in terms of sine and cosine:
$$ \tan(x) = \frac{\sin(x)}{\cos(x)} $$
Substituting this into the equation gives:
$$ \cos(x) \cdot (-\tan(x)) = -\cos(x) \cdot \frac{\sin(x)}{\cos(x)} $$
The cosines cancel out (given that $\cos(x) \neq 0$):
$$ -\sin(x) $$
- Final Formulation
Now we equate the left and right sides of the equation:
$$ -\sin(x) = -\sin(x) $$
This shows that the original equation is indeed true for all values of $x$ where the functions are defined.
The equation is valid for all values of $x$ where the functions are defined.
More Information
This result shows the underlying symmetry and periodicity of trigonometric functions. In particular, using co-function identities simplifies the solving process significantly.
Tips
- Failing to apply the trigonometric identities correctly.
- Forgetting to consider the domain restrictions of the functions involved.
AI-generated content may contain errors. Please verify critical information