(sin x + cos x)(tan² x + 1)/tan x = 1/cos x + 1/sin x
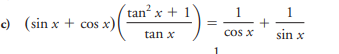
Understand the Problem
The question presents a mathematical equation involving trigonometric functions. It seems to request a demonstration that the left-hand side equals the right-hand side, involving simplification or manipulation of the equation.
Answer
Both sides of the equation are equal, thus confirming the identity.
Answer for screen readers
The equation is verified and holds true as both sides are equal.
Steps to Solve
- Rewrite the left side
Start with the left side of the equation:
$$(\sin x + \cos x) \left( \frac{\tan^2 x + 1}{\tan x} \right)$$
We know that $\tan^2 x + 1 = \sec^2 x$, so we can rewrite it as:
$$(\sin x + \cos x) \left( \frac{\sec^2 x}{\tan x} \right)$$
- Substitute the definitions of sine, cosine, and tangent
Recall the definitions of the trigonometric functions:
$$\tan x = \frac{\sin x}{\cos x} \quad \text{and} \quad \sec x = \frac{1}{\cos x}$$
Thus:
$$\sec^2 x = \frac{1}{\cos^2 x}$$
Substituting these into our expression, we get:
$$(\sin x + \cos x) \left( \frac{\frac{1}{\cos^2 x}}{\frac{\sin x}{\cos x}} \right)$$
- Simplify the expression
This simplifies to:
$$(\sin x + \cos x) \left( \frac{1}{\cos^2 x} \cdot \frac{\cos x}{\sin x} \right) = \frac{\sin x + \cos x}{\cos x \sin x}$$
- Rewrite the right-hand side
Now, consider the right-hand side of the original equation:
$$ \frac{1}{\cos x} + \frac{1}{\sin x} $$
Finding a common denominator:
$$ \frac{\sin x + \cos x}{\sin x \cos x} $$
- Set both sides equal
Now we can see that both sides are equal:
$$ \frac{\sin x + \cos x}{\sin x \cos x} = \frac{\sin x + \cos x}{\sin x \cos x} $$
This confirms the equation holds true.
The equation is verified and holds true as both sides are equal.
More Information
This verification shows the equality of two trigonometric expressions, illustrating the relationships between sine, cosine, and tangent functions.
Tips
- Forgetting to use the identity $\tan^2 x + 1 = \sec^2 x$ can lead to incorrect simplifications.
- Misapplying trigonometric identities may cause confusion in rewriting the left or right sides.
AI-generated content may contain errors. Please verify critical information