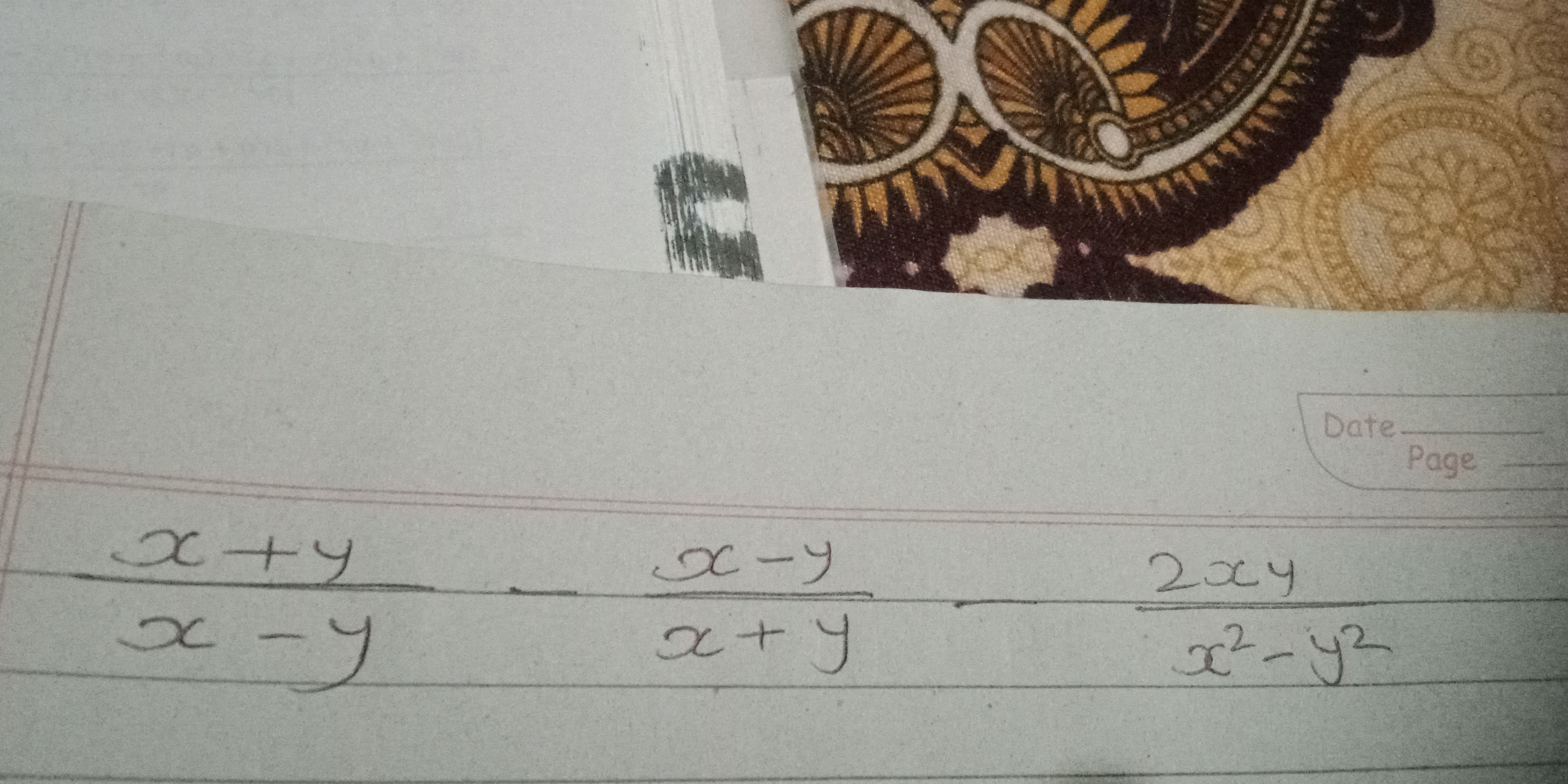
Simplify the following expressions: (x + y)/(x - y) and (x - y)/(x + y) and (2xy)/(x^2 - y^2).

Understand the Problem

The question involves algebraic expressions and their simplifications, particularly focusing on operations involving addition and subtraction of variables x and y, and it appears to explore the simplification of a fraction involving these variables.

Answer

1. $\frac{x + y}{x - y}$, 2. $\frac{x - y}{x + y}$, 3. $\frac{2xy}{(x + y)(x - y)}$

Steps to Solve

Simplifying the first expression: $\frac{x + y}{x - y}$

To simplify $\frac{x + y}{x - y}$, we can leave it as is since it cannot be simplified further without specific values for $x$ and $y$.

Simplifying the second expression: $\frac{x - y}{x + y}$

Similarly, $\frac{x - y}{x + y}$ also cannot be simplified further without specific values.

Simplifying the third expression: $\frac{2xy}{x^2 - y^2}$

The expression $x^2 - y^2$ can be factored using the difference of squares:

$$ x^2 - y^2 = (x + y)(x - y) $$

Thus, we rewrite the third expression:

$$ \frac{2xy}{x^2 - y^2} = \frac{2xy}{(x + y)(x - y)} $$

This is now in its simplest form, indicating that it cannot be simplified further without specific values.

The simplified forms of the expressions are:

$\frac{x + y}{x - y}$
$\frac{x - y}{x + y}$
$\frac{2xy}{(x + y)(x - y)}$

More Information

These expressions highlight important algebraic concepts including fractions and the difference of squares. It's important to remember that certain expressions cannot be simplified without specific values for the variables involved.

Tips

Assuming that a fraction can always be simplified: Always check for common factors before concluding that a fraction is in its simplest form.
Overlooking the difference of squares in the third expression: Remember to factor whenever you see a difference of squares.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!