Simplify the following expressions: 6. 3^0 ÷ (y^2 / y^2); 7. (3x^4)^2 * (x^{-1})^8; 8. (4x - 2xy) / x.

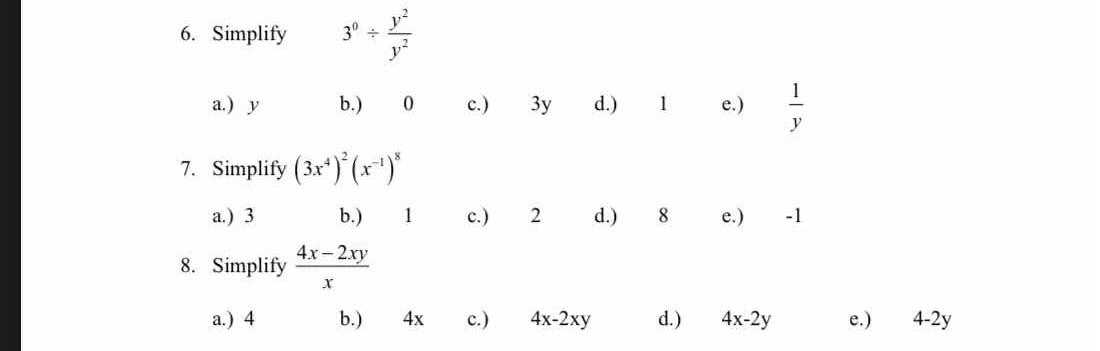
Understand the Problem

The question is asking to simplify several mathematical expressions, specifically focusing on problems involving exponents and algebraic fractions. This requires applying knowledge of algebraic rules, such as the laws of exponents and simplification techniques.

Answer

6. 1, 7. 9, 8. $ 4 - 2y $

Steps to Solve

Simplify the first expression

For the expression ( 3^0 \div \left(\frac{y^2}{y^2}\right) ):
- Recall that ( 3^0 = 1 )
- The fraction simplifies as ( \frac{y^2}{y^2} = 1 ) (for ( y \neq 0 )).
- Thus, we have: $$ 1 \div 1 = 1 $$
Evaluate the second expression

For the expression ( (3x^4)^2 \cdot (x^{-1})^8 ):
- Start with ( (3x^4)^2 = 3^2 \cdot (x^4)^2 = 9x^8 ).
- Next, ( (x^{-1})^8 = x^{-8} ).
- Now combine them: $$ 9x^8 \cdot x^{-8} = 9x^{8 - 8} = 9x^0 = 9 \cdot 1 = 9 $$
Simplify the third expression

For the expression ( \frac{4x - 2xy}{x} ):
- Factor the numerator: ( 4x - 2xy = 2x(2 - y) ).
- Divide by ( x ): $$ \frac{2x(2 - y)}{x} = 2(2 - y) = 4 - 2y $$

1
9
( 4 - 2y )

More Information

For the first expression, anything raised to the power of zero is 1.
For the second expression, the product property of exponents was essential to simplify.
In the last expression, factoring and then canceling terms allowed for an easier simplification.

Tips

Confusing ( 3^0 ) with a different value (it is always 1).
Forgetting to apply the property of exponents correctly when multiplying terms.
Not factoring correctly or neglecting to cancel common terms when simplifying fractions.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!