Simplify the following expression with exponents: 9z^(-2) / z^(-1).
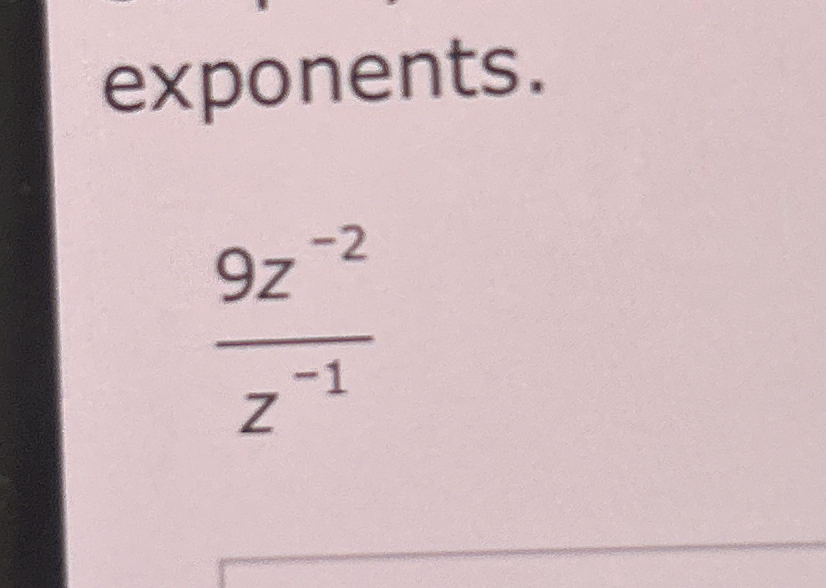
Understand the Problem
The question is asking for the simplification of the expression involving exponents, specifically the fraction of two expressions with variable z raised to different powers.
Answer
The simplified expression is $\frac{9}{z}$.
Answer for screen readers
The simplified expression is:
$$ \frac{9}{z} $$
Steps to Solve
- Set up the expression
We start with the expression:
$$ \frac{9z^{-2}}{z^{-1}} $$
- Use the property of exponents
Recall that when dividing identical bases, we subtract the exponents:
$$ \frac{a^m}{a^n} = a^{m-n} $$
So we will apply this property to $z^{-2}$ and $z^{-1}$:
$$ z^{-2 - (-1)} = z^{-2 + 1} $$
- Calculate the exponent
Now, perform the calculation of the exponent:
$$ -2 + 1 = -1 $$
So we simplify the expression to:
$$ 9z^{-1} $$
- Rewrite with positive exponent
To express this with a positive exponent, we can rewrite $z^{-1}$ as $\frac{1}{z}$:
$$ 9z^{-1} = \frac{9}{z} $$
The simplified expression is:
$$ \frac{9}{z} $$
More Information
This simplification uses the laws of exponents, which help to rearrange expressions involving powers. For example, $a^{-n}$ can be rewritten as $\frac{1}{a^n}$, which is a fundamental property in algebra.
Tips
- Forgetting to subtract the exponents correctly when dividing.
- Misinterpreting the negative exponents, leading to confusion about the final form.
AI-generated content may contain errors. Please verify critical information