Simplify the following algebraic expressions: (a) 3a × 2 - 2 × 5a (b) (8 × b × a) × (-4 × a × a × b)
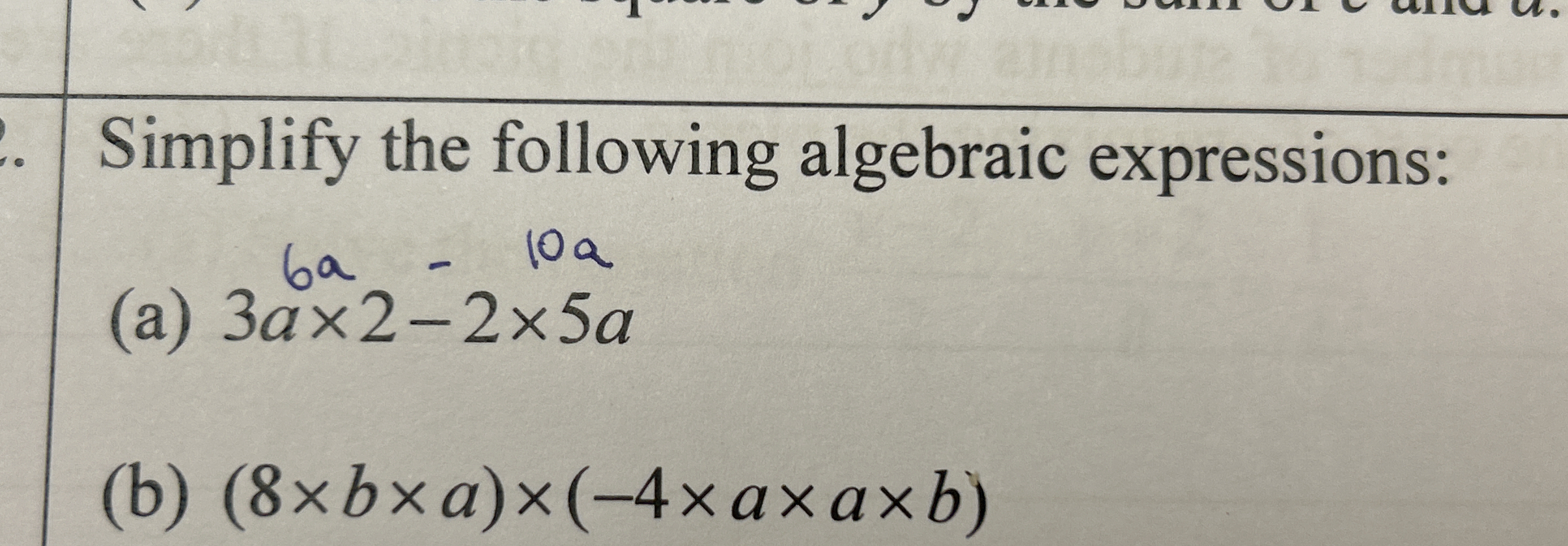
Understand the Problem
The question is asking us to simplify two algebraic expressions: (a) 3a × 2 - 2 × 5a and (b) (8 × b × a) × (-4 × a × a × b). We will perform arithmetic operations and combine like terms where necessary.
Answer
(a) \(-4a\) (b) \(-32b^2a^3\)
Answer for screen readers
(a) (-4a)
(b) (-32b^2a^3)
Steps to Solve
- Simplify the first expression (a)
Start with the expression (3a \times 2 - 2 \times 5a).
Calculate (3a \times 2): $$ 3a \times 2 = 6a $$
Calculate (2 \times 5a): $$ 2 \times 5a = 10a $$
Now substitute back into the expression: $$ 6a - 10a $$
Combine like terms: $$ 6a - 10a = -4a $$
- Simplify the second expression (b)
Consider the expression ((8 \times b \times a) \times (-4 \times a \times a \times b)).
First, multiply the coefficients and the variables separately:
- Coefficients: (8 \times -4 = -32)
- Variables: (b \times b = b^2) and (a \times a^2 = a^3)
Now combine them: $$ -32 \times b^2 \times a^3 $$
- Final expressions
The simplified results for both expressions are: (a) (-4a)
(b) (-32b^2a^3)
(a) (-4a)
(b) (-32b^2a^3)
More Information
The simplifications involve applying the distributive property and combining like terms. These basic operations are foundational for manipulating algebraic expressions.
Tips
- Forgetting to apply the negative sign when multiplying.
- Not combining like terms properly, especially with coefficients.
- Misplacing multiplication operations when dealing with multiple variable terms.
AI-generated content may contain errors. Please verify critical information