Simplify the following algebraic expressions. (a) 20 - 4b × 5ab (b) (6 × a × b) × (-2 × x × a)
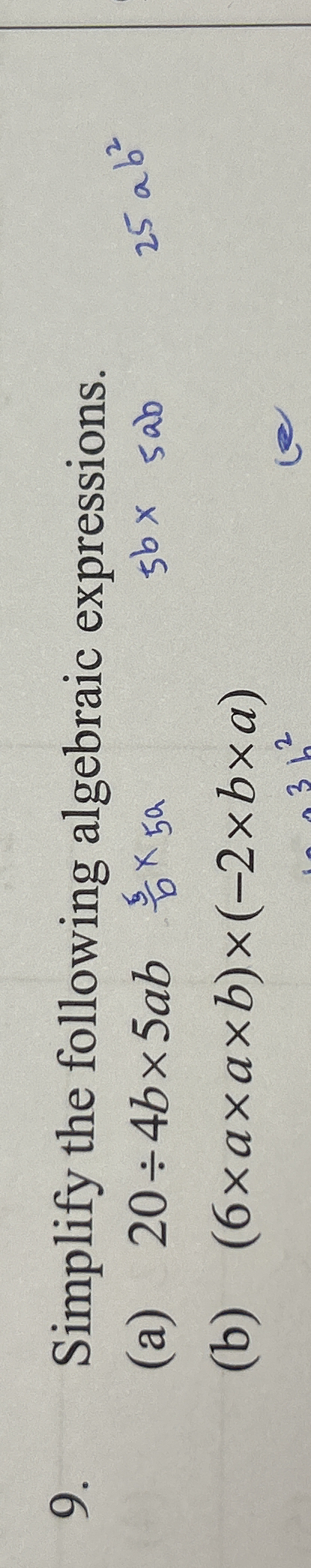
Understand the Problem
The question is asking to simplify two given algebraic expressions indicated as (a) and (b) in a mathematical context. The first expression involves the coefficients and variables, while the second expression appears to involve a product of variables.
Answer
(a) \(20 - 20ab\) (b) \(-12a^2bx\)
Answer for screen readers
(a) (20 - 20ab)
(b) (-12a^2bx)
Steps to Solve
- Simplifying Expression (a)
Start by substituting the multiplication in the expression (20 - 4b \times 5ab).
This becomes:
$$ 20 - 20ab $$
where (4b \times 5ab = 20ab).
- Final Form for Expression (a)
The simplified form of expression (a) is:
$$ 20 - 20ab $$
- Simplifying Expression (b)
Now move on to expression (b). We have:
$$(6 \times a \times b) \times (-2 \times x \times a)$$
- Rearranging the Terms
Combine the coefficients and like terms:
$$ (6 \times -2) \times (a \times a) \times b \times x $$
This results in:
$$ -12a^2bx $$
- Final Form for Expression (b)
Thus, the simplified form of expression (b) is:
$$ -12a^2bx $$
(a) (20 - 20ab)
(b) (-12a^2bx)
More Information
The expressions have been simplified by applying the distributive property and combining like terms. These types of simplifications are essential for solving more complex algebraic equations.
Tips
- Not following the order of operations may lead to incorrect simplifications.
- Forgetting to distribute coefficients can result in an incomplete solution.
AI-generated content may contain errors. Please verify critical information