Simplify the expression (x^2 + x - 2) / (x^2 + 4x - 5).
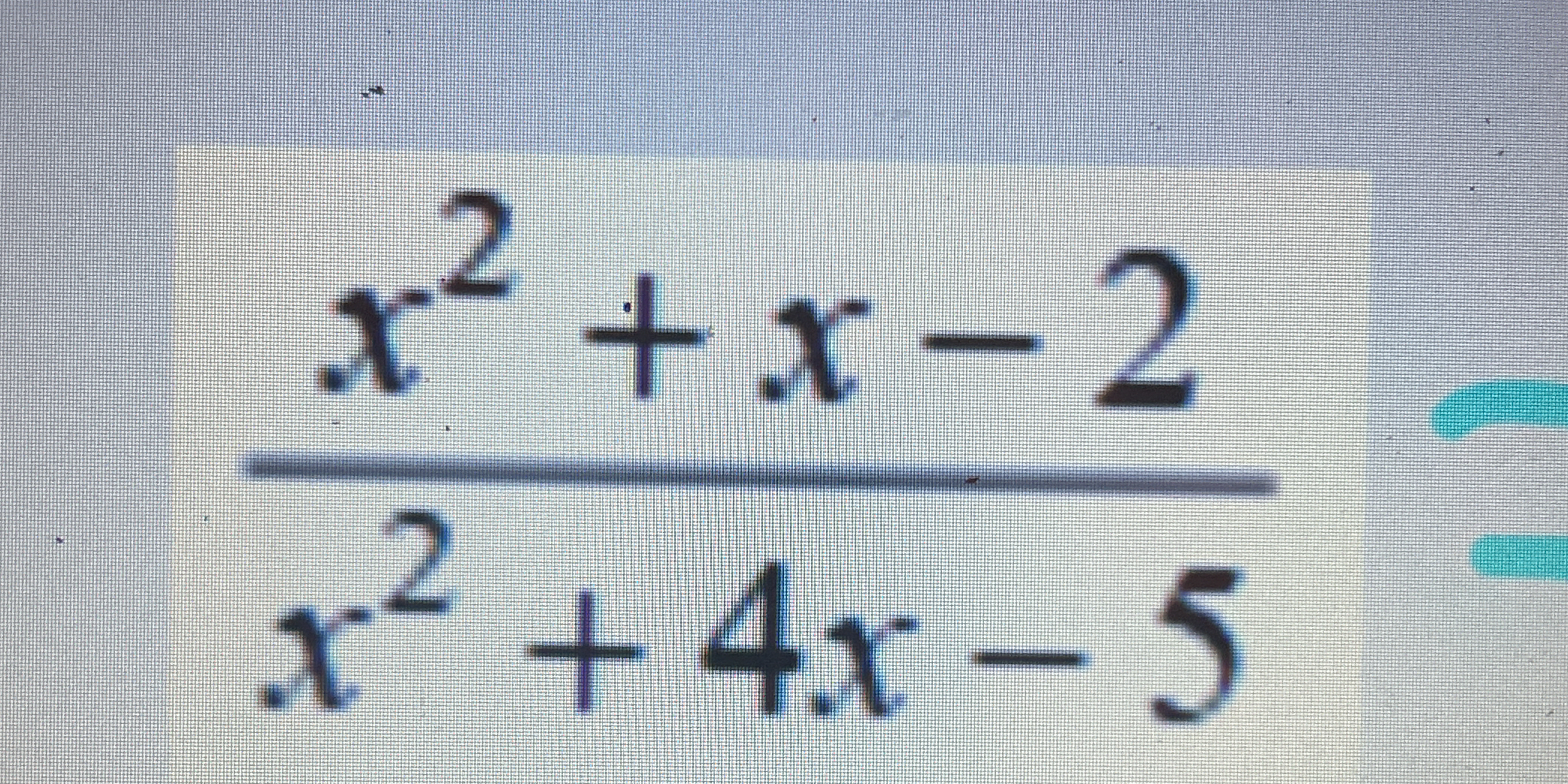
Understand the Problem
The question presents a rational expression that needs to be simplified. The goal is to factor both the numerator and denominator, then reduce the expression if possible.
Answer
The simplified expression is \( \frac{x + 2}{x + 5} \).
Answer for screen readers
The simplified expression is ( \frac{x + 2}{x + 5} ).
Steps to Solve
-
Factor the numerator
The numerator is (x^2 + x - 2). To factor it, we look for two numbers that multiply to (-2) (the constant term) and add to (1) (the coefficient of (x)). The numbers (2) and (-1) work. Thus, $$ x^2 + x - 2 = (x + 2)(x - 1). $$ -
Factor the denominator
The denominator is (x^2 + 4x - 5). We need two numbers that multiply to (-5) and add to (4). The numbers (5) and (-1) fit. Therefore, we have $$ x^2 + 4x - 5 = (x + 5)(x - 1). $$ -
Rewrite the rational expression
Substituting the factored forms back into the original expression gives us: $$ \frac{x^2 + x - 2}{x^2 + 4x - 5} = \frac{(x + 2)(x - 1)}{(x + 5)(x - 1)}. $$ -
Cancel common factors
Both the numerator and denominator contain the factor ((x - 1)). We can cancel it, provided (x \neq 1): $$ \frac{(x + 2) \cancel{(x - 1)}}{(x + 5) \cancel{(x - 1)}} = \frac{x + 2}{x + 5}, \quad \text{for } x \neq 1. $$ -
Final expression
The expression simplifies to: $$ \frac{x + 2}{x + 5}. $$
The simplified expression is ( \frac{x + 2}{x + 5} ).
More Information
This simplification shows how factoring can help reduce rational expressions. It’s crucial to remember to identify when a factor can be canceled, keeping in mind any restrictions on the variable that arise from the cancellation.
Tips
- Forgetting to check for restrictions: When canceling, always note that the canceled factor must not be equal to zero (i.e., (x \neq 1)).
- Incorrectly factoring: Carefully check that the numbers chosen for factoring are accurate and fulfill both multiplication and addition conditions.
AI-generated content may contain errors. Please verify critical information