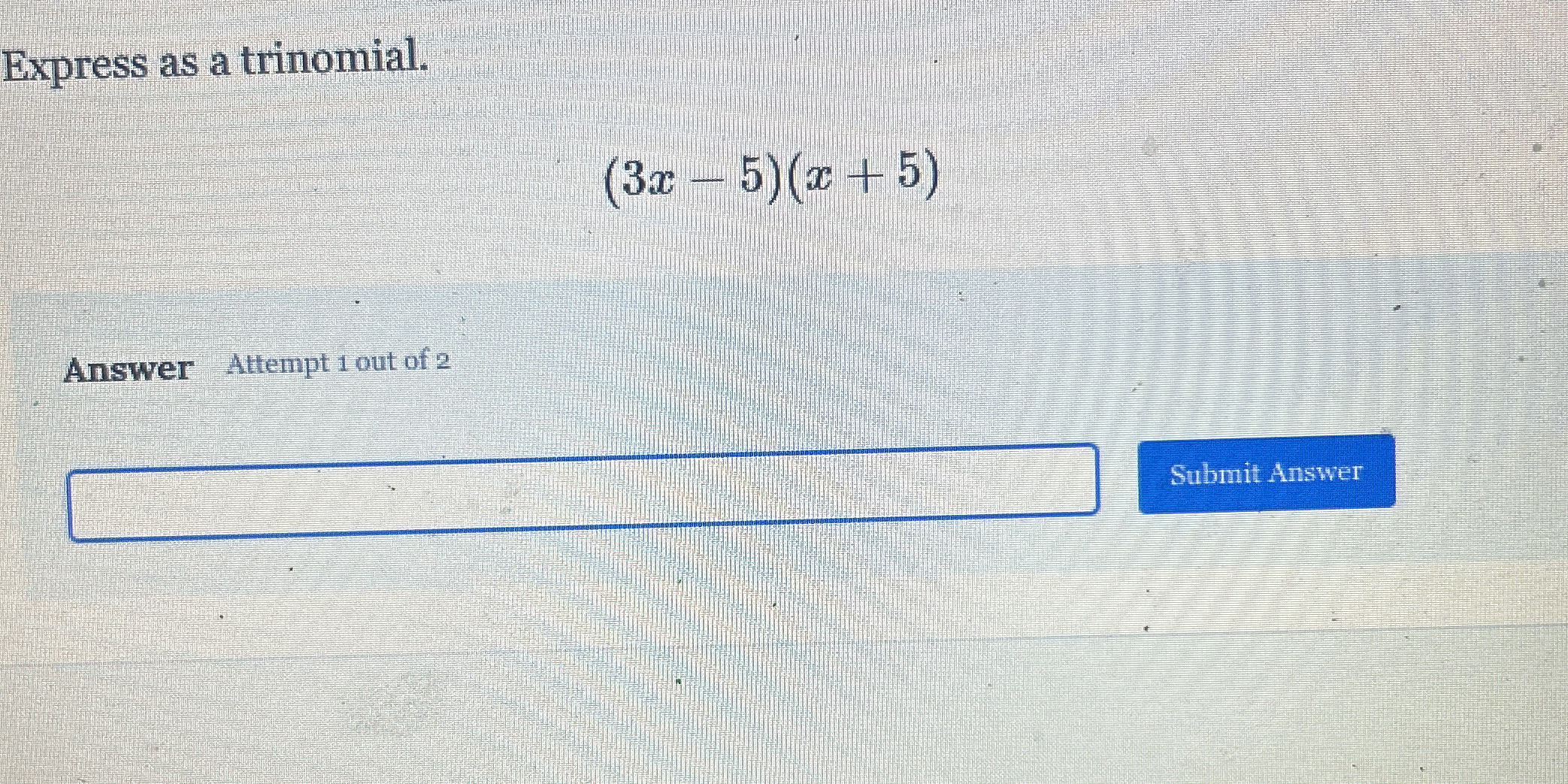
Express as a trinomial: (3x - 5)(x + 5)
Understand the Problem
The question is asking to multiply two binomials, (3x - 5) and (x + 5), and express the result as a trinomial.
Answer
The trinomial is $3x^2 + 10x - 25$.
Answer for screen readers
The resulting trinomial is $3x^2 + 10x - 25$.
Steps to Solve
-
Use the Distributive Property To multiply the binomials $(3x - 5)$ and $(x + 5)$, use the distributive property (also known as FOIL: First, Outer, Inner, Last).
-
Multiply the First Terms Multiply the first terms in each binomial: $$3x \cdot x = 3x^2$$
-
Multiply the Outer Terms Next, multiply the outer terms: $$3x \cdot 5 = 15x$$
-
Multiply the Inner Terms Now, multiply the inner terms: $$-5 \cdot x = -5x$$
-
Multiply the Last Terms Lastly, multiply the last terms: $$-5 \cdot 5 = -25$$
-
Combine Like Terms Now, add all the results together: $$3x^2 + 15x - 5x - 25$$
Combine like terms ($15x - 5x$): $$3x^2 + 10x - 25$$
The resulting trinomial is $3x^2 + 10x - 25$.
More Information
Multiplying binomials is a foundational skill in algebra that helps with understanding polynomial expressions and functions. The FOIL method specifically simplifies the multiplication of two binomials by ensuring that each term is accounted for.
Tips
- Forgetting to multiply all terms in the binomials can lead to missing parts of the product.
- Confusing the signs when multiplying negative numbers can result in errors, especially when working with the last terms.
AI-generated content may contain errors. Please verify critical information