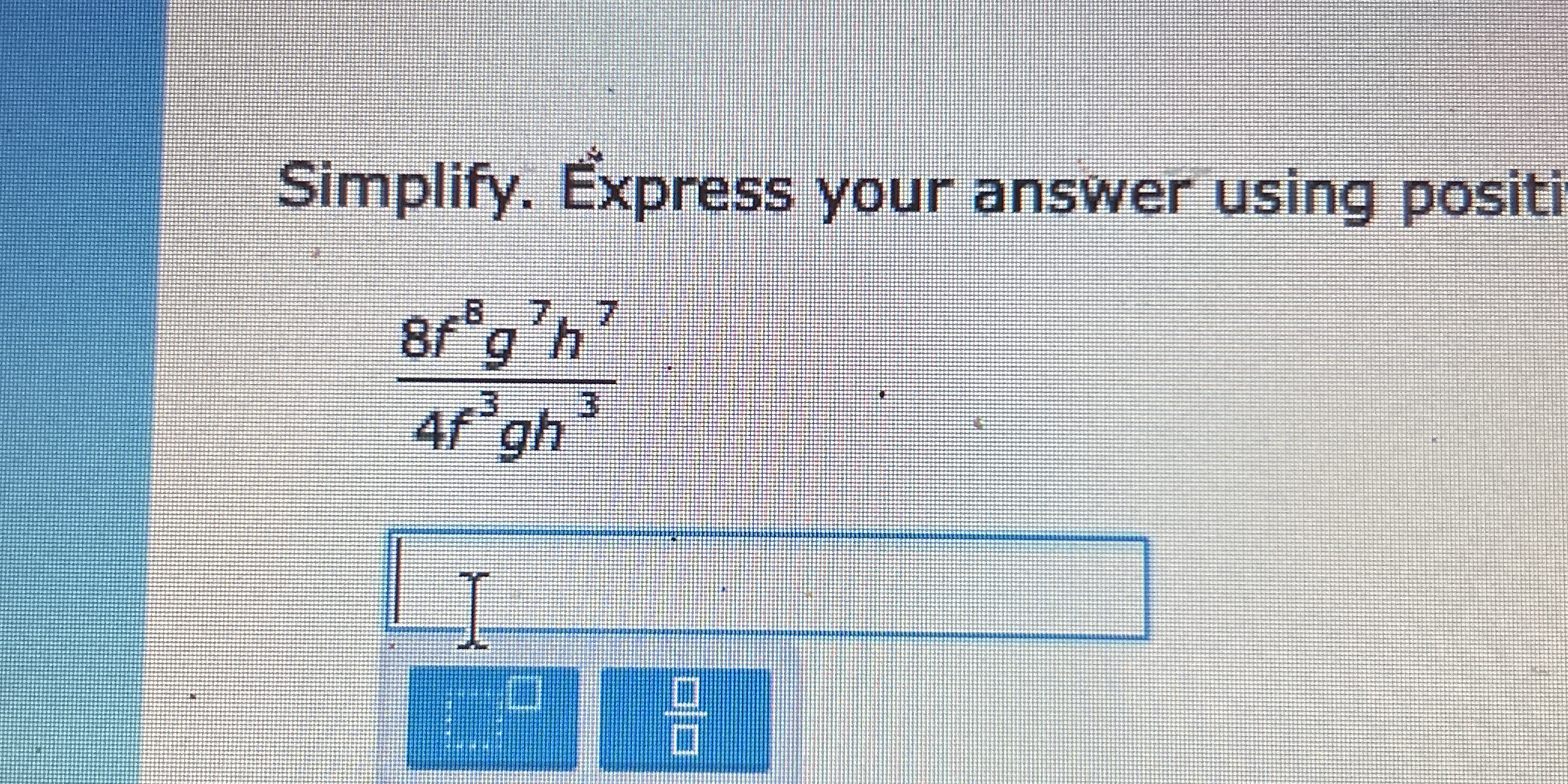
Simplify the expression 8g^7h^7 / 4g^3h^3. Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the given rational expression involving variables and exponents. We will identify like terms and apply the laws of exponents to reduce the expression.
Answer
The simplified expression is \( 2g^{4}h^{4} \).
Answer for screen readers
The simplified expression is ( 2g^{4}h^{4} ).
Steps to Solve
-
Identify the coefficients and variables The expression is given as $\frac{8g^{7}h^{7}}{4g^{3}h^{3}}$. Identify the coefficients (8 and 4) and variables ($g$ and $h$) along with their exponents.
-
Simplify the coefficients Divide the coefficients: $$ \frac{8}{4} = 2 $$
-
Apply the laws of exponents to the variable $g$ Use the rule $\frac{a^m}{a^n} = a^{m-n}$: $$ g^{7-3} = g^{4} $$
-
Apply the laws of exponents to the variable $h$ Similarly for $h$: $$ h^{7-3} = h^{4} $$
-
Combine the results Combine the simplified coefficient and variables: $$ 2g^{4}h^{4} $$
The simplified expression is ( 2g^{4}h^{4} ).
More Information
The result ( 2g^{4}h^{4} ) indicates that the original expression has been reduced by factoring out common elements from the numerator and denominator, illustrating the laws of exponents efficiently.
Tips
- Confusing the rules of exponents, such as subtracting instead of adding exponents.
- Forgetting to simplify the coefficients before handling the variables.
AI-generated content may contain errors. Please verify critical information