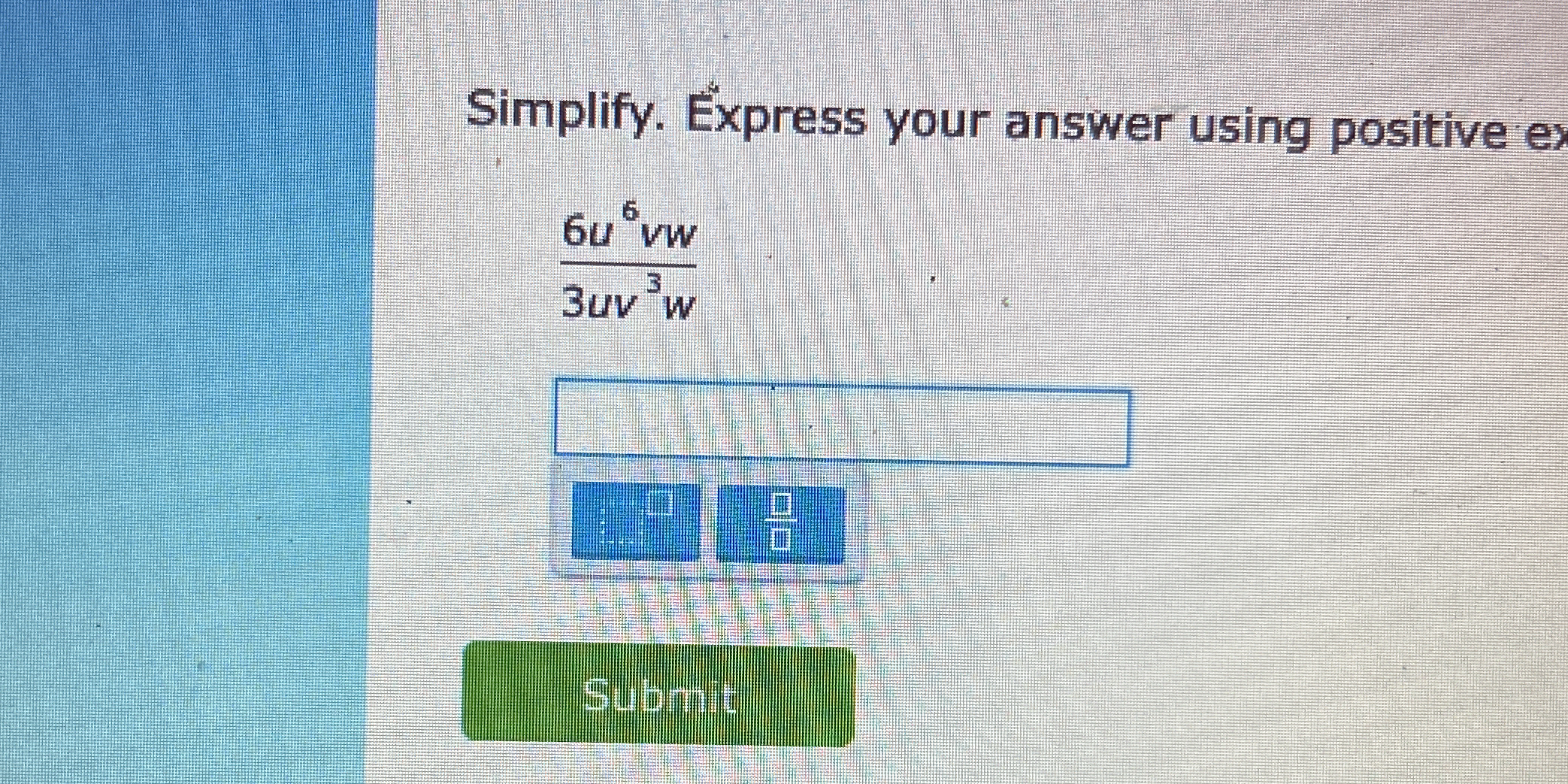
Simplify the expression 6u^6vw / 3uv^3w
Understand the Problem
The question is asking to simplify the expression \( \frac{6u^{6}vw}{3uv^{3}w} \) and express the answer using positive exponents.
Answer
The simplified expression is $$ \frac{2u^{5}}{v^{2}} $$.
Answer for screen readers
The simplified expression is $$ \frac{2u^{5}}{v^{2}} $$.
Steps to Solve
-
Divide the coefficients The coefficient in the numerator is 6, and in the denominator, it is 3. To simplify, calculate: $$ \frac{6}{3} = 2 $$
-
Simplify the variable ( u ) The exponent of ( u ) in the numerator is 6 and in the denominator, it is 1 (as there's no exponent shown). Therefore, subtract the exponents: $$ u^{6-1} = u^{5} $$
-
Simplify the variable ( v ) The exponent of ( v ) in the numerator is 1 (as it is ( v ) which is equivalent to ( v^{1} )), and in the denominator, it is 3. So, subtract the exponents: $$ v^{1-3} = v^{-2} $$
-
Simplify the variable ( w ) The exponent of ( w ) in both the numerator and denominator is 1. When dividing, we get: $$ w^{1-1} = w^{0} = 1 $$
-
Combine the results Now combine all the simplified parts together: $$ 2u^{5}v^{-2} $$
-
Express with positive exponents To express the result with positive exponents, rewrite ( v^{-2} ) as ( \frac{1}{v^{2}} ): $$ 2u^{5} \cdot \frac{1}{v^{2}} = \frac{2u^{5}}{v^{2}} $$
The simplified expression is $$ \frac{2u^{5}}{v^{2}} $$.
More Information
This expression represents a single fraction combining all variables with their respective coefficients and exponents. The simplification process included reducing coefficients and handling exponents correctly.
Tips
- Forgetting to subtract exponents correctly when dealing with the same base.
- Neglecting to convert negative exponents into positive form in the final result.
- Incorrectly simplifying coefficients and factors.
AI-generated content may contain errors. Please verify critical information