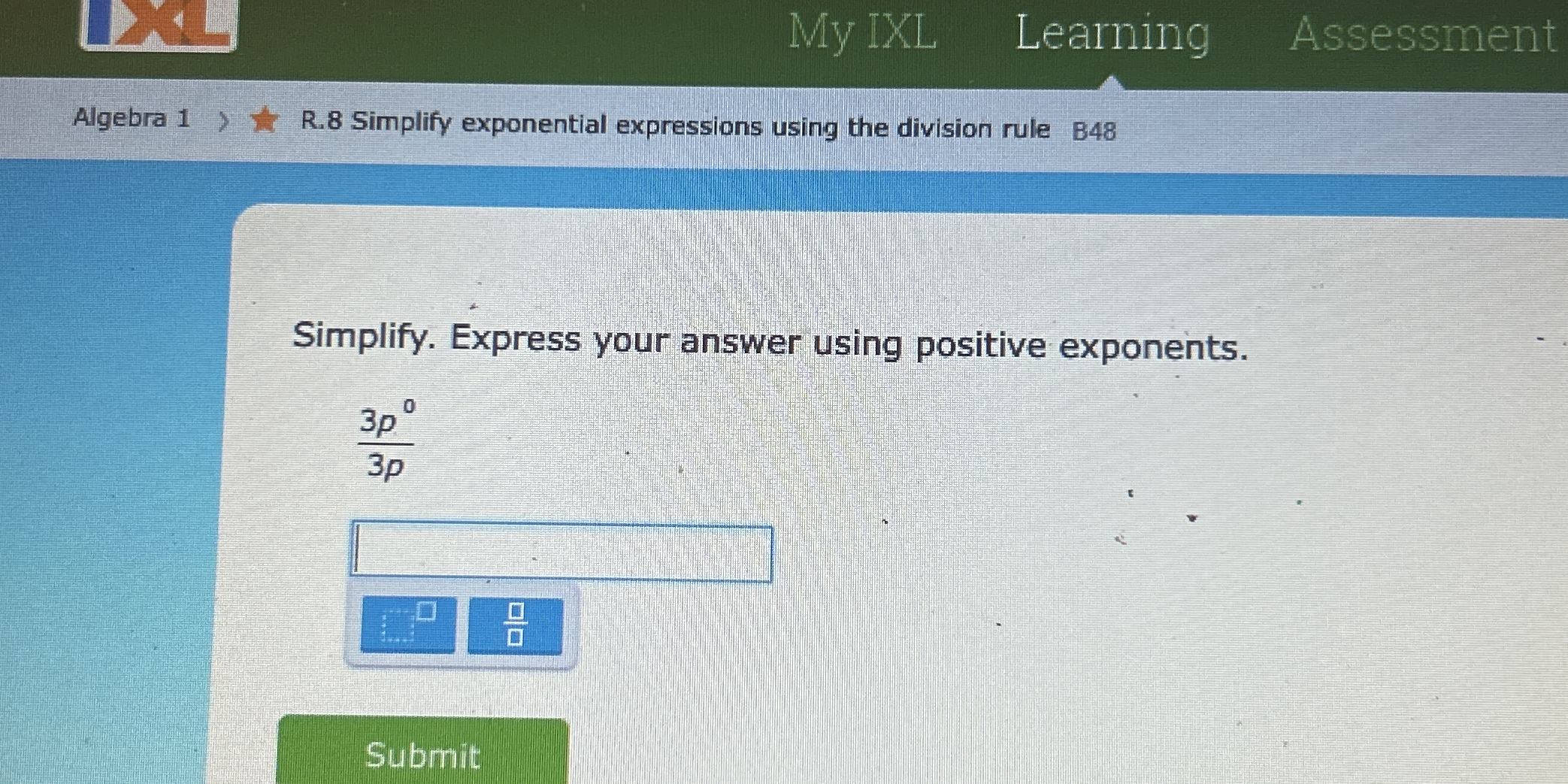
Simplify the expression 3p^0 / 3p using positive exponents.
Understand the Problem
The question is asking to simplify the expression 3p^0 / 3p using the division rule for exponents and to express the answer with positive exponents.
Answer
The simplified expression is \( p^{-1} \).
Answer for screen readers
The simplified expression is ( p^{-1} ).
Steps to Solve
-
Recognize the Exponent Rules We know that any non-zero number raised to the power of zero is equal to one. Therefore, we start with: $$ p^0 = 1 $$
-
Substitute the Value of ( p^0 ) Substituting this back into the expression gives us: $$ \frac{3 \cdot 1}{3p} $$
-
Simplify the Division of Constants Next, we can simplify the constants: $$ \frac{3}{3} = 1 $$ So the expression now becomes: $$ \frac{1}{p} $$
-
Express with Positive Exponents To express this with a positive exponent, we rewrite: $$ \frac{1}{p} = p^{-1} $$
The simplified expression is ( p^{-1} ).
More Information
The expression ( p^{-1} ) signifies that ( p ) is in the denominator, as ( p^{-n} ) means ( \frac{1}{p^n} ). This simplification is useful in algebraic manipulations.
Tips
- Forgetting that ( p^0 = 1 ) can lead to incorrect simplifications.
- Confusing the rules of exponents, especially when to use negative exponents.
AI-generated content may contain errors. Please verify critical information