Simplify the expression 2√3 / √(5 - √3).
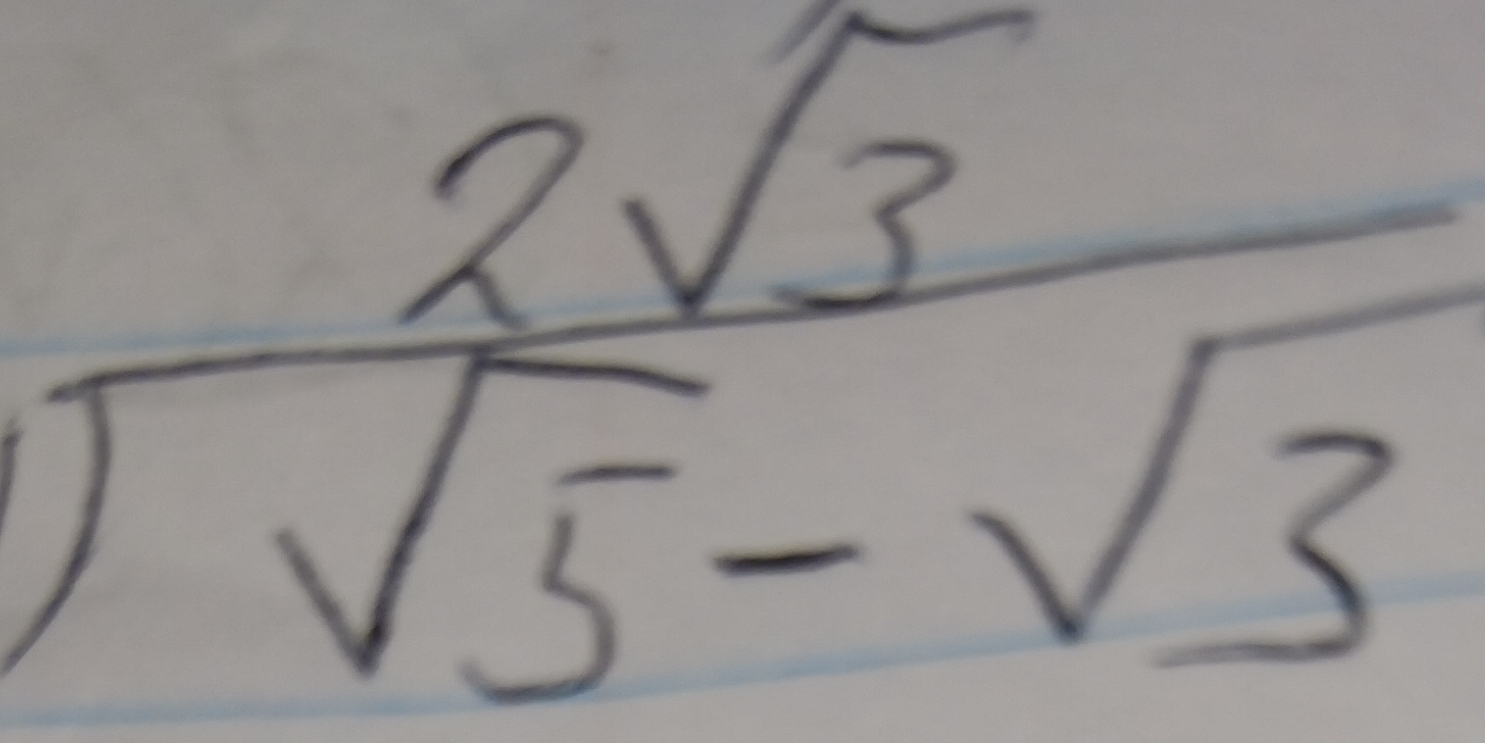
Understand the Problem
The question is asking to simplify a mathematical expression involving square roots. The expression provided is a fraction with the numerator and denominator both containing square roots, specifically involving 2√3 and √(5 - √3). We will simplify this step by step.
Answer
The final simplified expression is: $$ \frac{2\sqrt{22(15 + 3\sqrt{3})}}{22} $$
Answer for screen readers
The final simplified expression is: $$ \frac{2\sqrt{22(15 + 3\sqrt{3})}}{22} $$
Steps to Solve
-
Identify the Expression The expression to simplify is $\frac{2\sqrt{3}}{\sqrt{5 - \sqrt{3}}}$.
-
Rationalize the Denominator To remove the square root from the denominator, multiply both the numerator and denominator by $\sqrt{5 + \sqrt{3}}$ (the conjugate of the denominator). $$ \frac{2\sqrt{3} \cdot \sqrt{5 + \sqrt{3}}}{\sqrt{5 - \sqrt{3}} \cdot \sqrt{5 + \sqrt{3}}} $$
-
Simplify the Denominator Use the difference of squares formula: $a^2 - b^2 = (a + b)(a - b)$. Thus, $$ \sqrt{5 - \sqrt{3}} \cdot \sqrt{5 + \sqrt{3}} = \sqrt{(5)^2 - (\sqrt{3})^2} = \sqrt{25 - 3} = \sqrt{22} $$
-
Simplify the Numerator Multiply the numerator: $$ 2\sqrt{3} \cdot \sqrt{5 + \sqrt{3}} = 2\sqrt{3(5 + \sqrt{3})} = 2\sqrt{15 + 3\sqrt{3}} $$
-
Combine Results The simplified expression is: $$ \frac{2\sqrt{15 + 3\sqrt{3}}}{\sqrt{22}} $$
-
Final Simplified Form This can be rewritten as: $$ \frac{2\sqrt{15 + 3\sqrt{3}}}{\sqrt{22}} \cdot \frac{\sqrt{22}}{\sqrt{22}} = \frac{2\sqrt{22(15 + 3\sqrt{3})}}{22} $$
The final simplified expression is: $$ \frac{2\sqrt{22(15 + 3\sqrt{3})}}{22} $$
More Information
This simplification involves the steps of rationalizing the denominator and applying properties of square roots, which are key techniques in algebra. Simplifying expressions is useful in various mathematical applications, such as solving equations and evaluating limits.
Tips
- Forgetting to multiply by the conjugate, which keeps the denominator from being rationalized.
- Not simplifying both the numerator and denominator fully, which may lead to a more complex form.
AI-generated content may contain errors. Please verify critical information