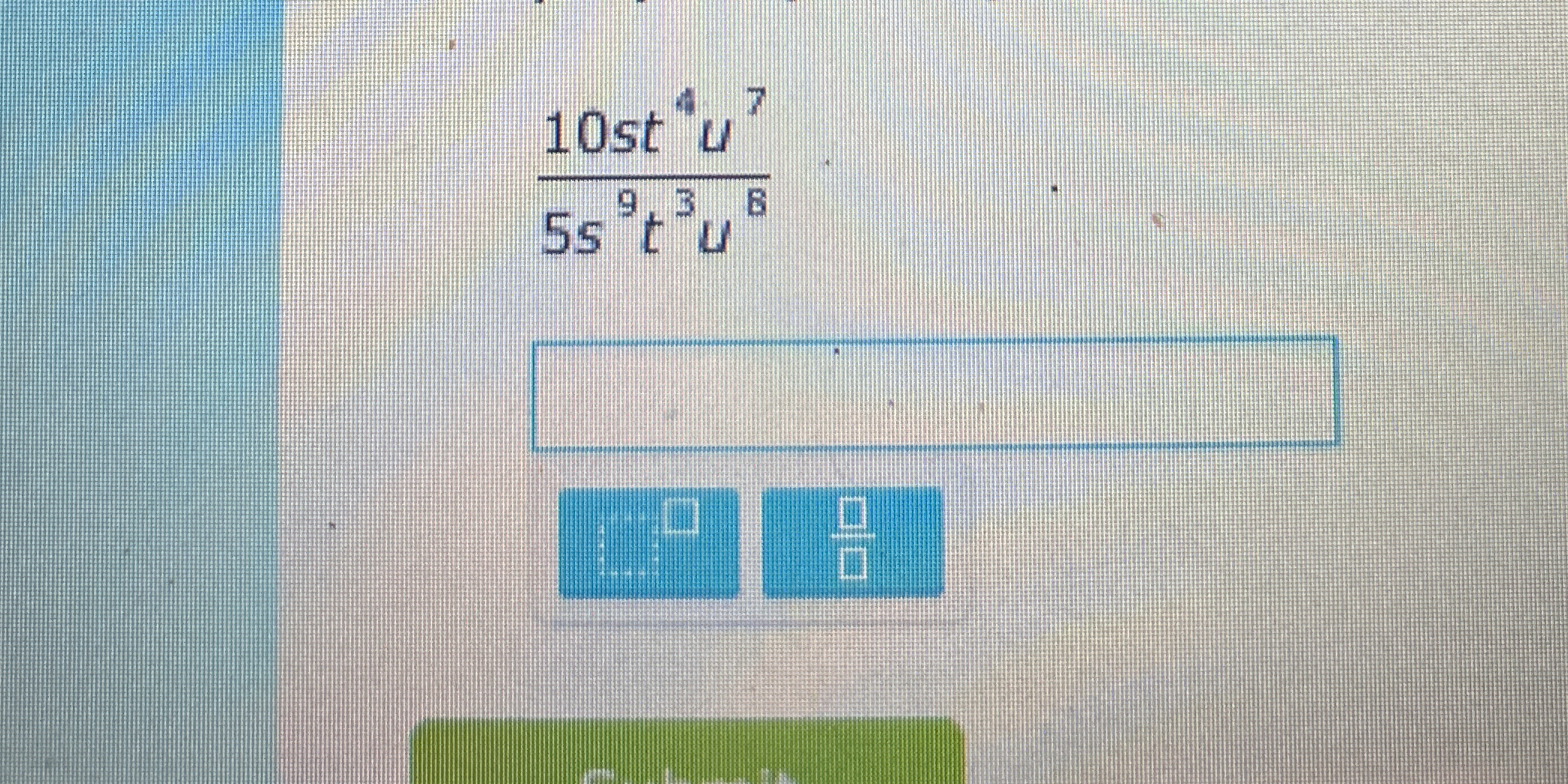
Simplify the expression (10st^4u^7) / (5st^9u^6).
Understand the Problem
The question presents a mathematical expression to simplify, which involves variables and exponents. It requires performing algebraic operations to reduce the expression.
Answer
The simplified expression is \( \frac{2u}{t^5} \).
Answer for screen readers
The simplified expression is ( \frac{2u}{t^5} ).
Steps to Solve
- Simplify the coefficients
Divide the coefficients (10) and (5): $$ \frac{10}{5} = 2 $$
- Simplify the (s) terms
Since there is no (s) in the numerator, keep the original (s) from the denominator. Thus we have: $$ \frac{s^1}{s^1} = s^{1-1} = s^0 = 1 $$
- Simplify the (t) terms
Subtract the exponents of (t): $$ \frac{t^4}{t^9} = t^{4-9} = t^{-5} $$
- Simplify the (u) terms
Subtract the exponents of (u): $$ \frac{u^7}{u^6} = u^{7-6} = u^1 = u $$
- Combine all simplified parts
Now combine all the simplified parts into one expression: $$ 2t^{-5}u $$
To express (t^{-5}) in the denominator: $$ = \frac{2u}{t^5} $$
The simplified expression is ( \frac{2u}{t^5} ).
More Information
This expression represents the result of dividing two algebraic expressions involving variables and their exponents. When simplifying expressions, remember to handle coefficients and variables independently.
Tips
- Forgetting to simplify coefficients separately.
- Not applying the exponent rules correctly when dividing variables.
- Overlooking that (s^0 = 1).
AI-generated content may contain errors. Please verify critical information