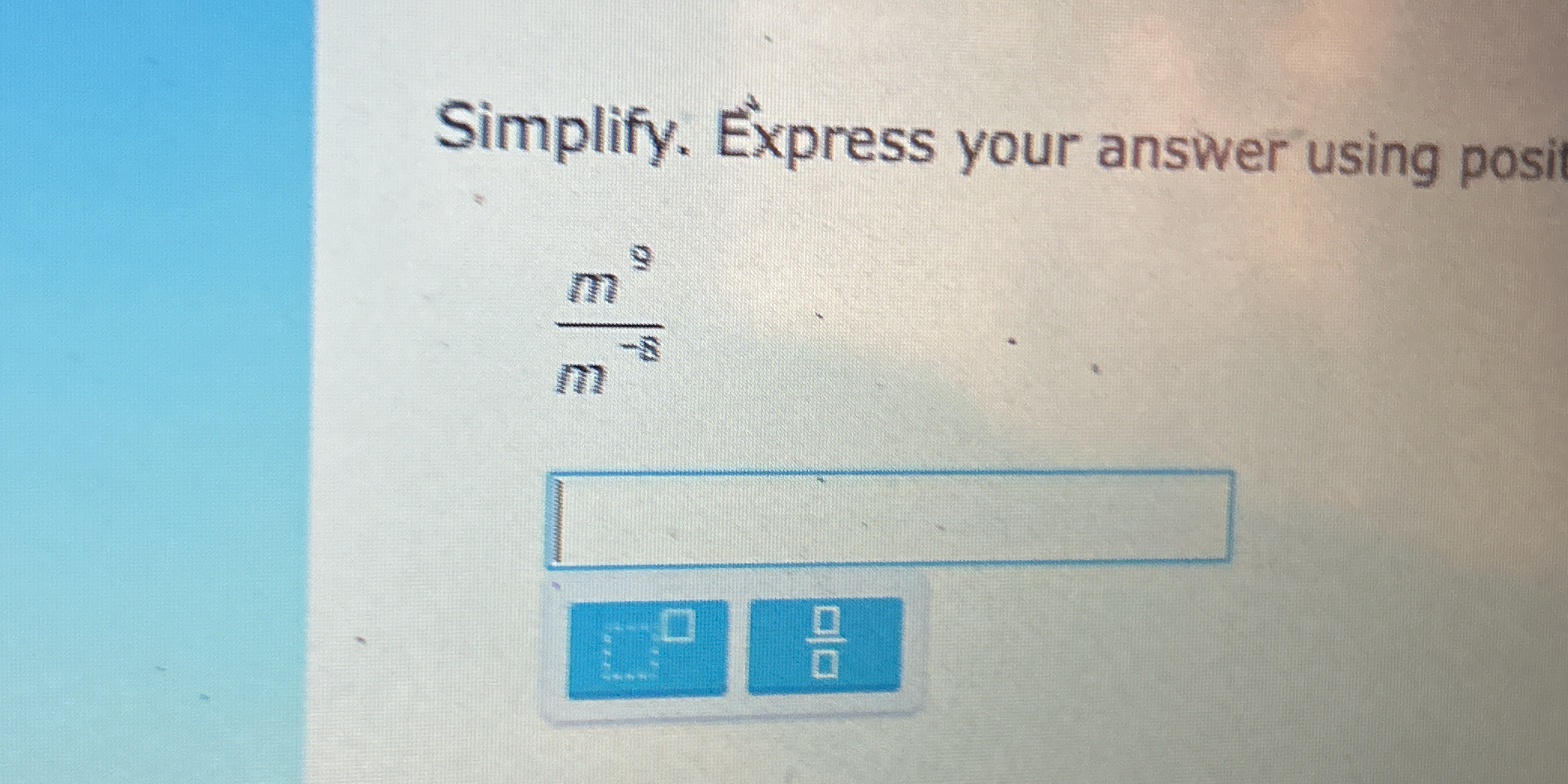
Simplify m^9 / m^-5. Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression m^{9} / m^{-5} and express the answer using positive exponents.
Answer
The simplified expression is $m^{14}$.
Answer for screen readers
The simplified expression is: $m^{14}$.
Steps to Solve
-
Simplify the expression using the exponent rules
First, rewrite the expression:
$$ \frac{m^{9}}{m^{-5}} $$
Using the rule of exponents that states $\frac{a^m}{a^n} = a^{m-n}$, we can simplify:
$$ m^{9 - (-5)} = m^{9 + 5} $$ -
Perform the arithmetic operation on the exponents
Now calculate the exponent:
$$ 9 + 5 = 14 $$
Thus, we have:
$$ m^{14} $$ -
Final result with positive exponents
The expression is now simplified to:
$$ m^{14} $$
The simplified expression is: $m^{14}$.
More Information
When simplifying expressions involving exponents, it's important to remember that subtracting a negative is the same as adding. This is an application of the laws of exponents.
Tips
- Confusing $m^{-n}$ with $-m^{n}$. Remember that $m^{-n}$ means $\frac{1}{m^n}$, not negative $m^n$.
- Forgetting to properly simplify by following the exponent subtraction rule; ensure each step adheres to the exponent laws.
AI-generated content may contain errors. Please verify critical information