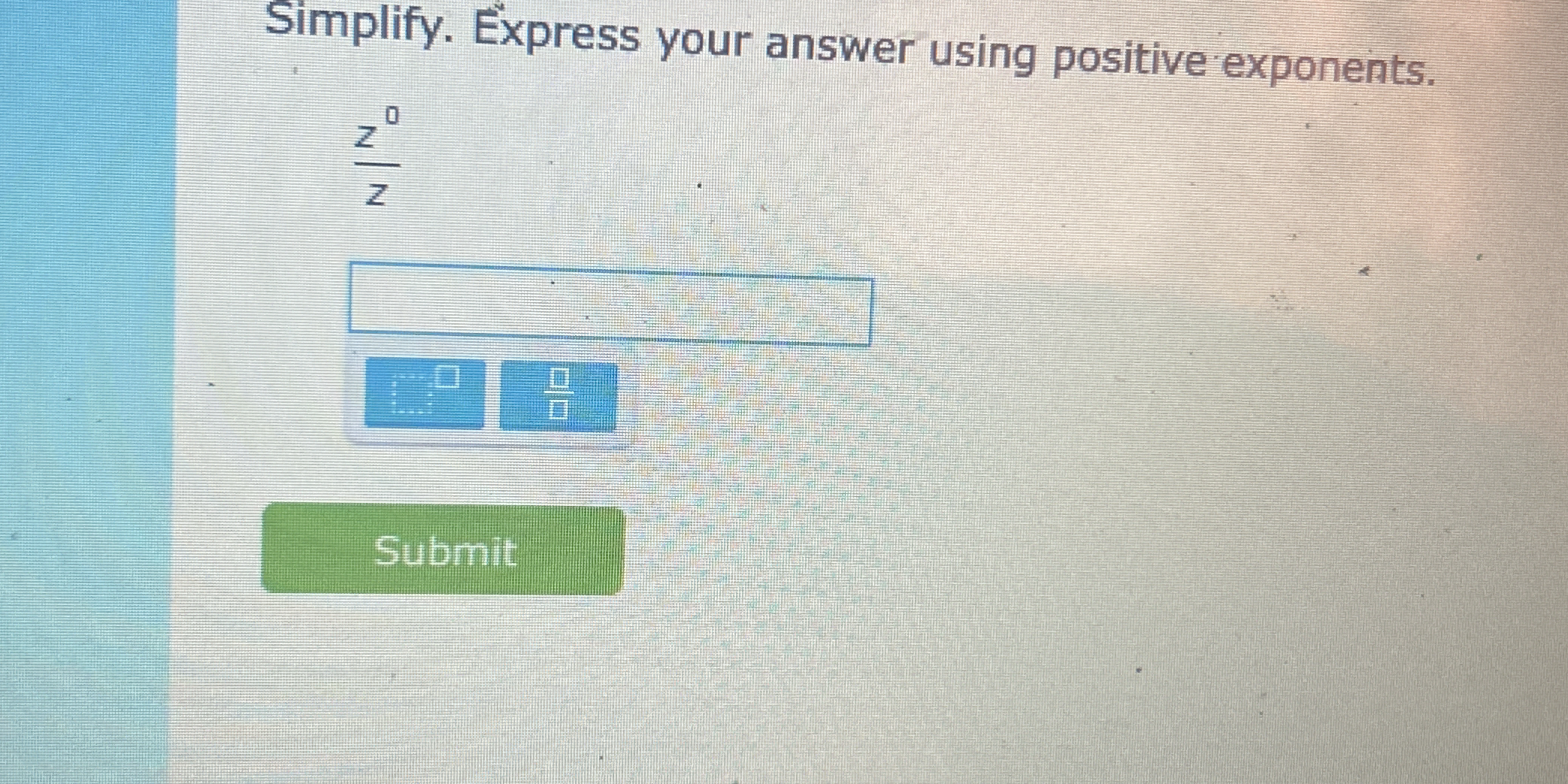
Simplify \( \frac{z^0}{z} \). Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression ( \frac{z^0}{z} ) and express the answer using positive exponents. The zero exponent rule states that any non-zero number raised to the power of zero equals one, which will simplify the fraction significantly.
Answer
The simplified expression is \( z^{-1} \).
Answer for screen readers
The simplified expression is ( z^{-1} ).
Steps to Solve
- Apply the Zero Exponent Rule
According to the zero exponent rule, any non-zero integer raised to the power of zero equals one. Therefore, we can simplify ( z^0 ) as follows: $$ z^0 = 1 $$
- Substitute the Simplified Value
Now, substitute ( z^0 ) with 1 in the original expression: $$ \frac{z^0}{z} = \frac{1}{z} $$
- Express with Positive Exponents
The expression ( \frac{1}{z} ) can be expressed using negative exponents. It becomes: $$ z^{-1} $$
The simplified expression is ( z^{-1} ).
More Information
The expression represents the reciprocal of ( z ). Using negative exponents is quite common in algebra, and it's crucial to understand that ( z^{-1} ) is equivalent to ( \frac{1}{z} ).
Tips
- Ignoring the Zero Exponent Rule: Some may forget that ( z^0 = 1 ) and mistakenly try to manipulate the expression without simplifying.
- Confusing Positive and Negative Exponents: It's important to recognize that ( \frac{1}{z} ) can be written as ( z^{-1} ).
AI-generated content may contain errors. Please verify critical information