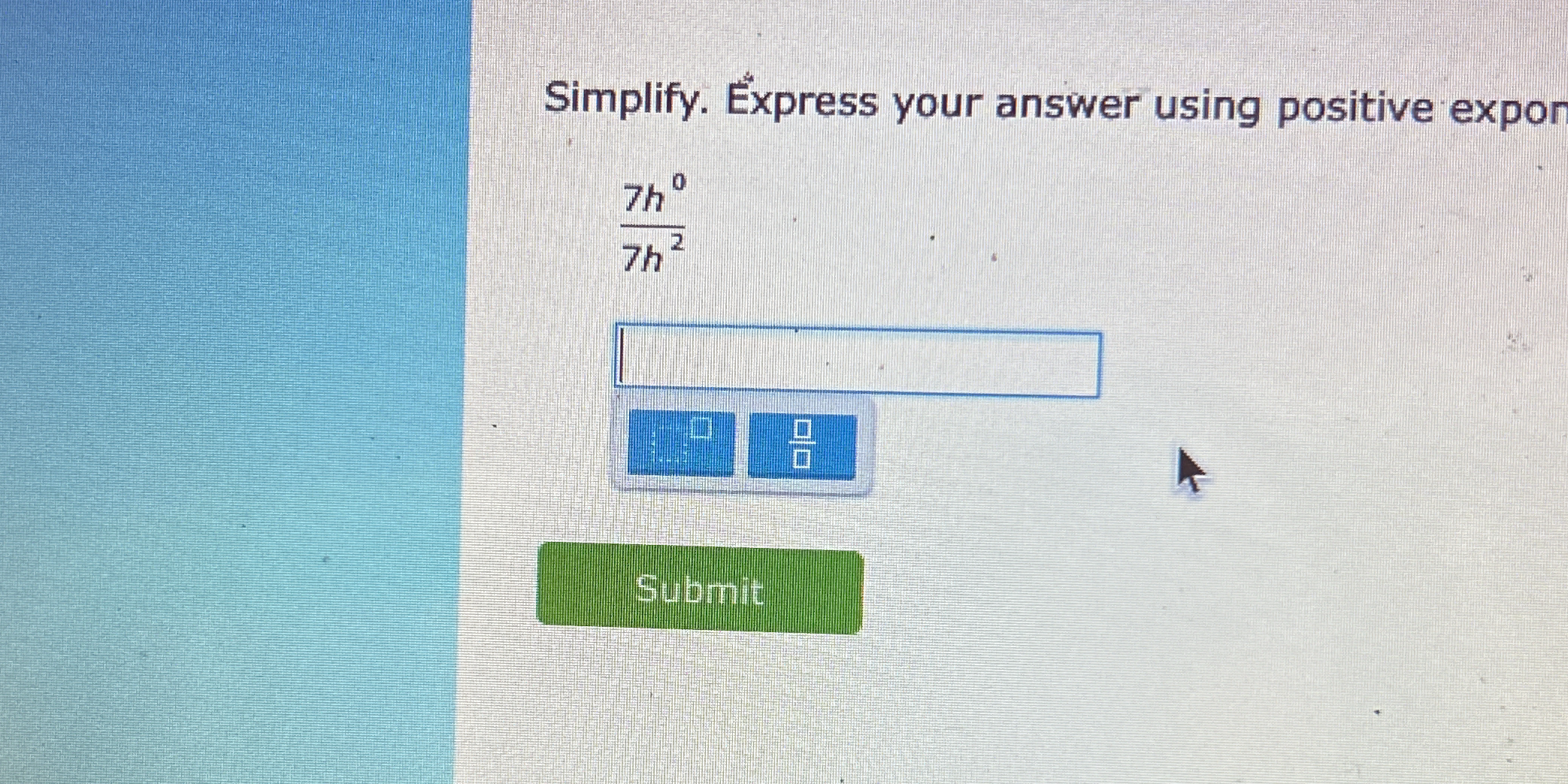
Simplify. Express your answer using positive exponents: 7h^0 / (7/h^2).
Understand the Problem
The question is asking to simplify the expression involving fractions and exponents, specifically to reduce the fraction 7h^0 / (7/h^2) and express the answer using positive exponents.
Answer
The simplified expression is \( h^{2} \).
Answer for screen readers
The simplified expression is ( h^{2} ).
Steps to Solve
-
Identify the expression to simplify We start with the expression: $$ \frac{7h^{0}}{\frac{7}{h^{2}}} $$
-
Rewrite the denominator We can rewrite the fraction in the denominator: $$ \frac{7}{h^{2}} = 7 \cdot h^{-2} $$
-
Simplify the complex fraction Now the expression becomes: $$ \frac{7h^{0}}{7h^{-2}} $$
-
Cancel out common factors Since $7$ appears in both the numerator and the denominator, it cancels out: $$ \frac{h^{0}}{h^{-2}} $$
-
Apply the exponent rule Using the rule for dividing exponents $\frac{a^{m}}{a^{n}} = a^{m-n}$: $$ h^{0 - (-2)} = h^{0 + 2} = h^{2} $$
-
Final simplification Since $h^{0} = 1$, we can confirm: $$ \frac{7h^{0}}{\frac{7}{h^{2}}} = h^{2} $$
The simplified expression is ( h^{2} ).
More Information
This simplification showcases how to manipulate exponents and fractions. The key result is that anything raised to the power of zero is 1, which facilitated cancellation in the process.
Tips
- Overlooking that ( h^{0} = 1 ) and thus incorrectly maintaining ( h^{0} ) in the final expression.
- Forgetting to apply the exponent subtraction correctly when dividing.
AI-generated content may contain errors. Please verify critical information