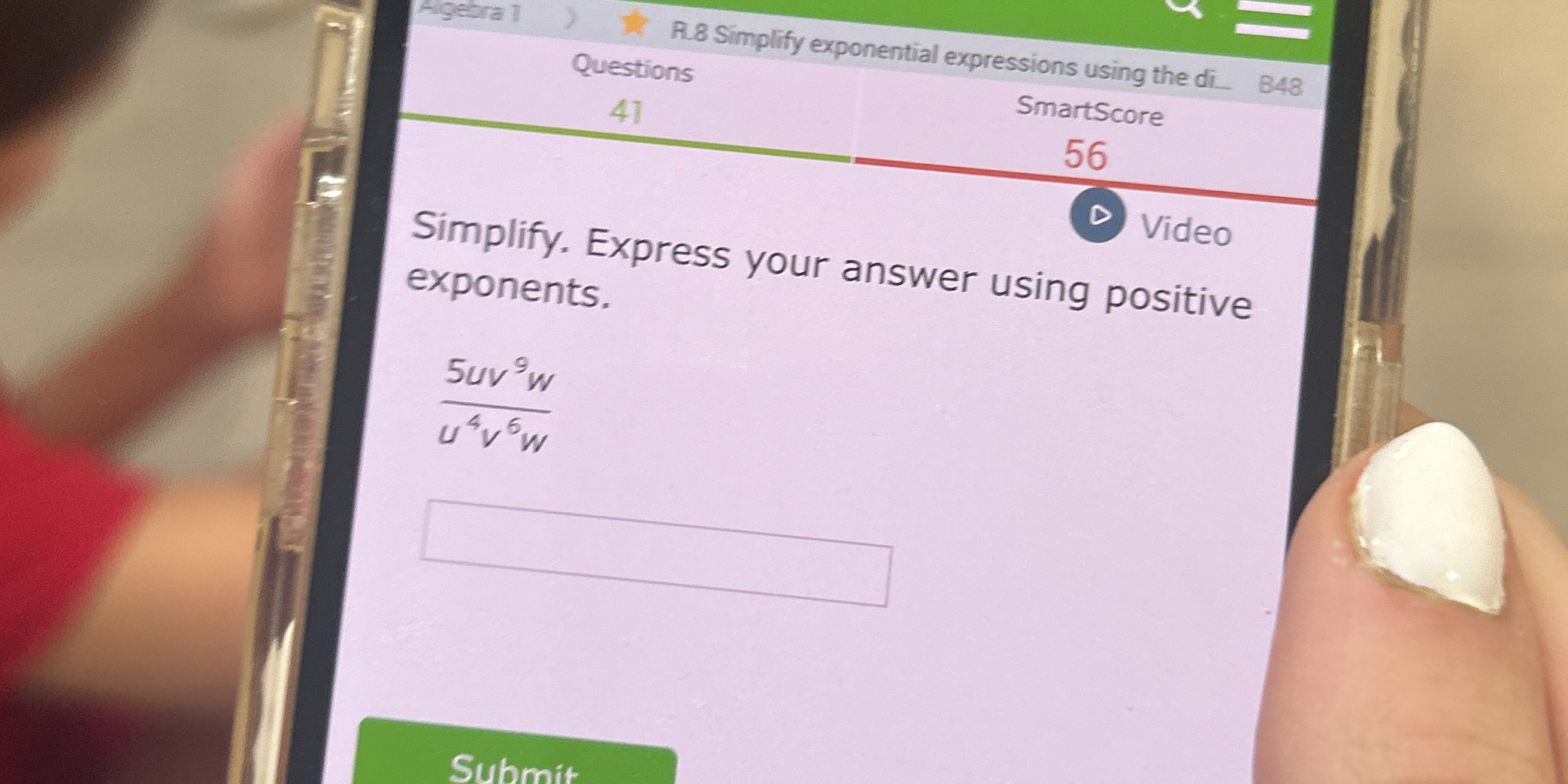
Simplify. Express your answer using positive exponents. 5u^1v^9w / u^4v^6w
Understand the Problem
The question is asking to simplify the expression given, which is a fraction involving exponentials with variables u, v, and w. We need to perform operations on the exponents and ensure that the final answer consists of only positive exponents.
Answer
The final simplified expression is $$ \frac{5v^3}{u^3} $$
Answer for screen readers
The simplified expression is
$$ \frac{5v^3}{u^3} $$
Steps to Solve
- Identify the expression
Look at the given fraction:
$$ \frac{5uv^9w}{u^4v^6w} $$
- Separate the terms
Rewrite the expression to separate the coefficients and the variables:
$$ \frac{5}{1} \cdot \frac{u}{u^4} \cdot \frac{v^9}{v^6} \cdot \frac{w}{w} $$
- Simplify the coefficients
Since there's no denominator for the coefficient, we keep it as it is:
$$ 5 $$
- Apply the quotient rule for exponents
For the variable $u$:
$$ \frac{u}{u^4} = u^{1-4} = u^{-3} $$
For the variable $v$:
$$ \frac{v^9}{v^6} = v^{9-6} = v^3 $$
For the variable $w$:
$$ \frac{w}{w} = w^{1-1} = w^0 = 1 $$
- Combine the simplified components
The expression now becomes:
$$ 5u^{-3}v^3 \cdot 1 = 5u^{-3}v^3 $$
- Rewrite with positive exponents
To express $u^{-3}$ with a positive exponent:
$$ 5 \cdot \frac{v^3}{u^3} $$
So the final simplified expression is:
$$ \frac{5v^3}{u^3} $$
The simplified expression is
$$ \frac{5v^3}{u^3} $$
More Information
This simplification involves using the properties of exponents, particularly the quotient rule, which states that when you divide like bases, you subtract the exponents.
Tips
- Forgetting to subtract exponents correctly when dealing with variables.
- Not simplifying coefficients properly.
- Ignoring that $w^0$ equals $1$, which can be omitted entirely.
AI-generated content may contain errors. Please verify critical information