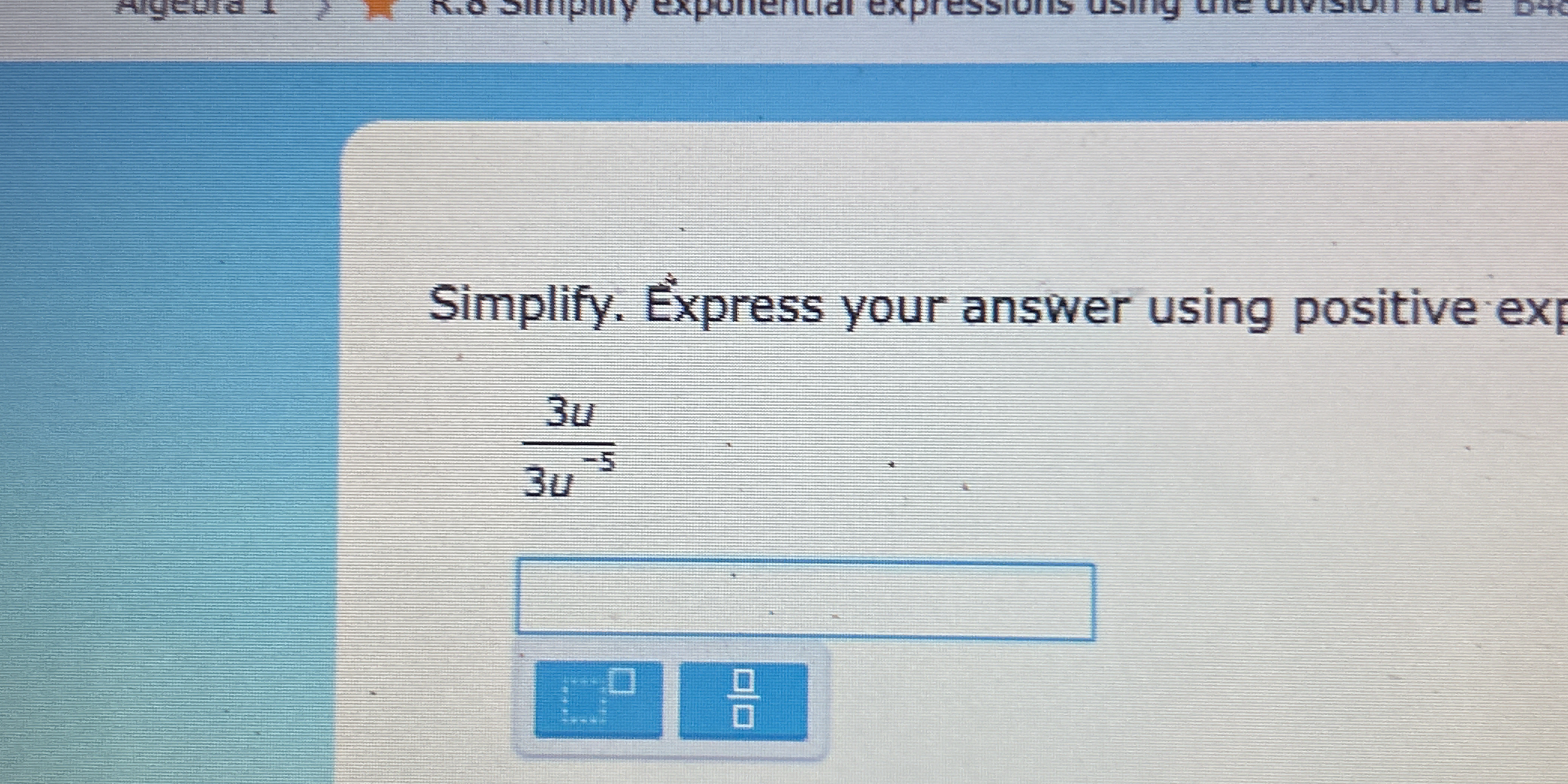
Simplify. Express your answer using positive exponents: (3u)/(3u^{-5})
Understand the Problem
The question asks us to simplify the given expression, which involves a fraction with exponential terms, and express the answer using positive exponents.
Answer
The simplified expression is \( u^6 \).
Answer for screen readers
The simplified expression is ( u^6 ).
Steps to Solve
-
Identify the expression We have the expression $$\frac{3u}{3u^{-5}}$$ to simplify.
-
Cancel common factors First, we can simplify the coefficients (the numerical parts): $$\frac{3}{3} = 1$$
Therefore, the expression now looks like: $$\frac{u}{u^{-5}}$$
-
Apply the rule for division of exponents Using the rule for dividing exponents, where $a^m / a^n = a^{m-n}$, we simplify: $$u^{1 - (-5)} = u^{1 + 5} = u^{6}$$
-
Final expression Since the problem asks to express the answer with positive exponents, our final simplified expression is: $$u^{6}$$
The simplified expression is ( u^6 ).
More Information
This expression represents a power of the variable ( u ), indicating that ( u ) is multiplied by itself six times. Exponential expressions are fundamental in algebra, as they simplify calculations and represent growth or decay in various applications.
Tips
- Forgetting to apply the negative exponent rule correctly. Remember that dividing by a negative exponent is equivalent to multiplying by the positive exponent.
- Not simplifying the coefficients first can lead to confusion. Always simplify the numerical parts before the variable parts.
AI-generated content may contain errors. Please verify critical information