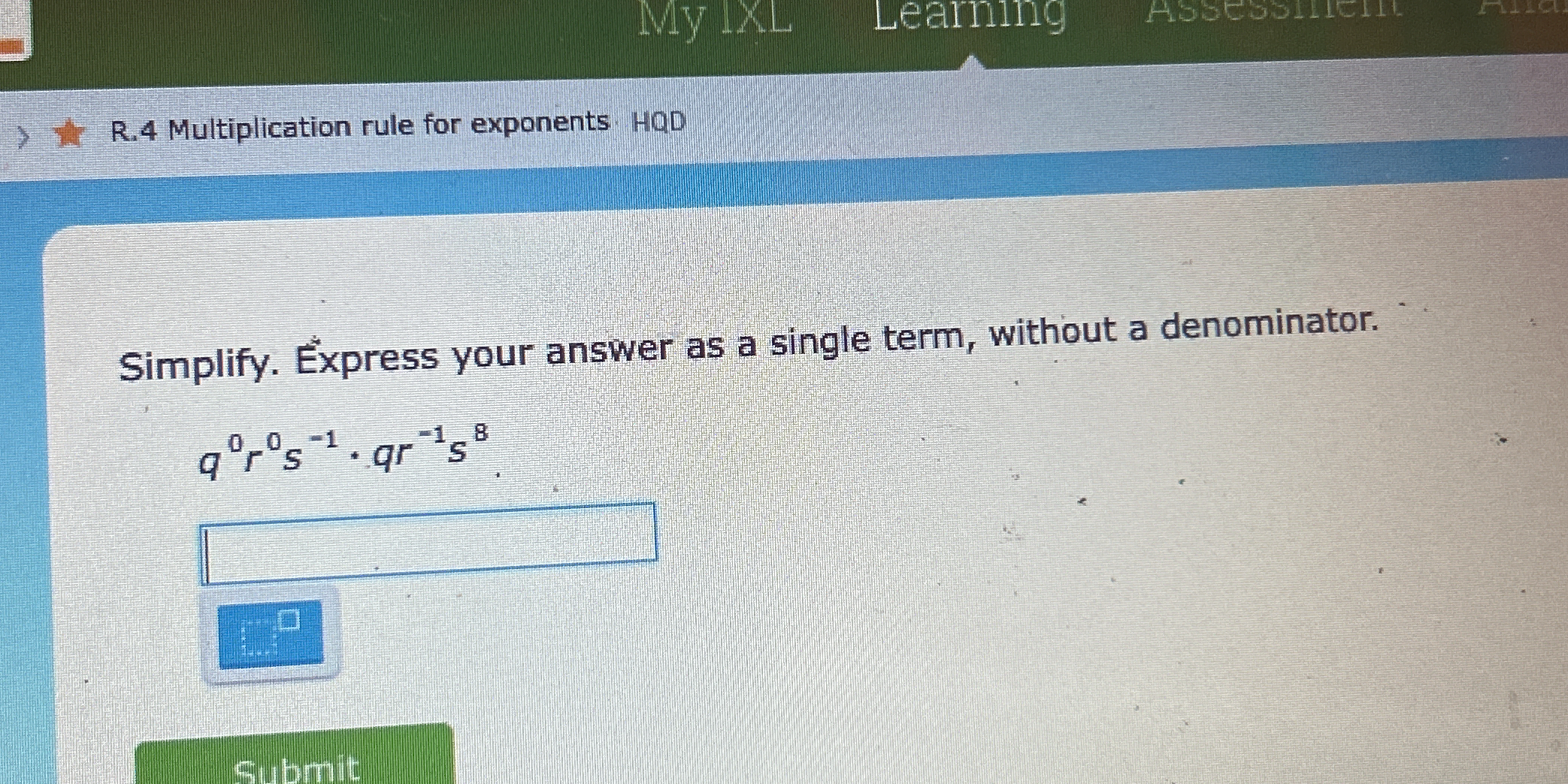
Simplify. Express your answer as a single term, without a denominator: q^0 * r^s * s^(-1) * q^r * s^8.
Understand the Problem
The question is asking to simplify the expression involving exponents and variables. It requires using the multiplication rule for exponents to combine the terms into a single term without a denominator.
Answer
The simplified expression is \( r \cdot q^{r^{-1}} \cdot s^{7} \).
Answer for screen readers
The final answer is ( r \cdot q^{r^{-1}} \cdot s^{7} ).
Steps to Solve
- Combine like terms for variable ( q )
The expression starts as ( q^0 r s^{-1} \cdot q^{r^{-1}} s^8 ).
Recall that ( q^0 = 1 ), so it can be ignored.
This leaves us with:
$$ r s^{-1} \cdot q^{r^{-1}} s^8 $$
- Apply the multiplication rule for exponents
Use the rule that states ( a^m \cdot a^n = a^{m+n} ) to combine the ( s ) terms.
Combine ( s^{-1} ) and ( s^8 ):
$$ s^{-1 + 8} = s^{7} $$
So now we have:
$$ r \cdot q^{r^{-1}} \cdot s^{7} $$
- Final result
The simplified expression is:
$$ r \cdot q^{r^{-1}} \cdot s^{7} $$
The final answer is ( r \cdot q^{r^{-1}} \cdot s^{7} ).
More Information
The variable ( q ) raised to the power ( r^{-1} ) means that if you have a specific value for ( r ), you can compute a numerical value for that term. Additionally, ( s^{7} ) indicates that ( s ) is raised to a positive exponent, highlighting that we have entirely removed the denominator.
Tips
- Forgetting that ( q^0 = 1 ) and not including it in the final expression.
- Misapplying the multiplication rule for exponents, particularly with negative exponents.
- Not combining terms correctly when dealing with different bases.
AI-generated content may contain errors. Please verify critical information