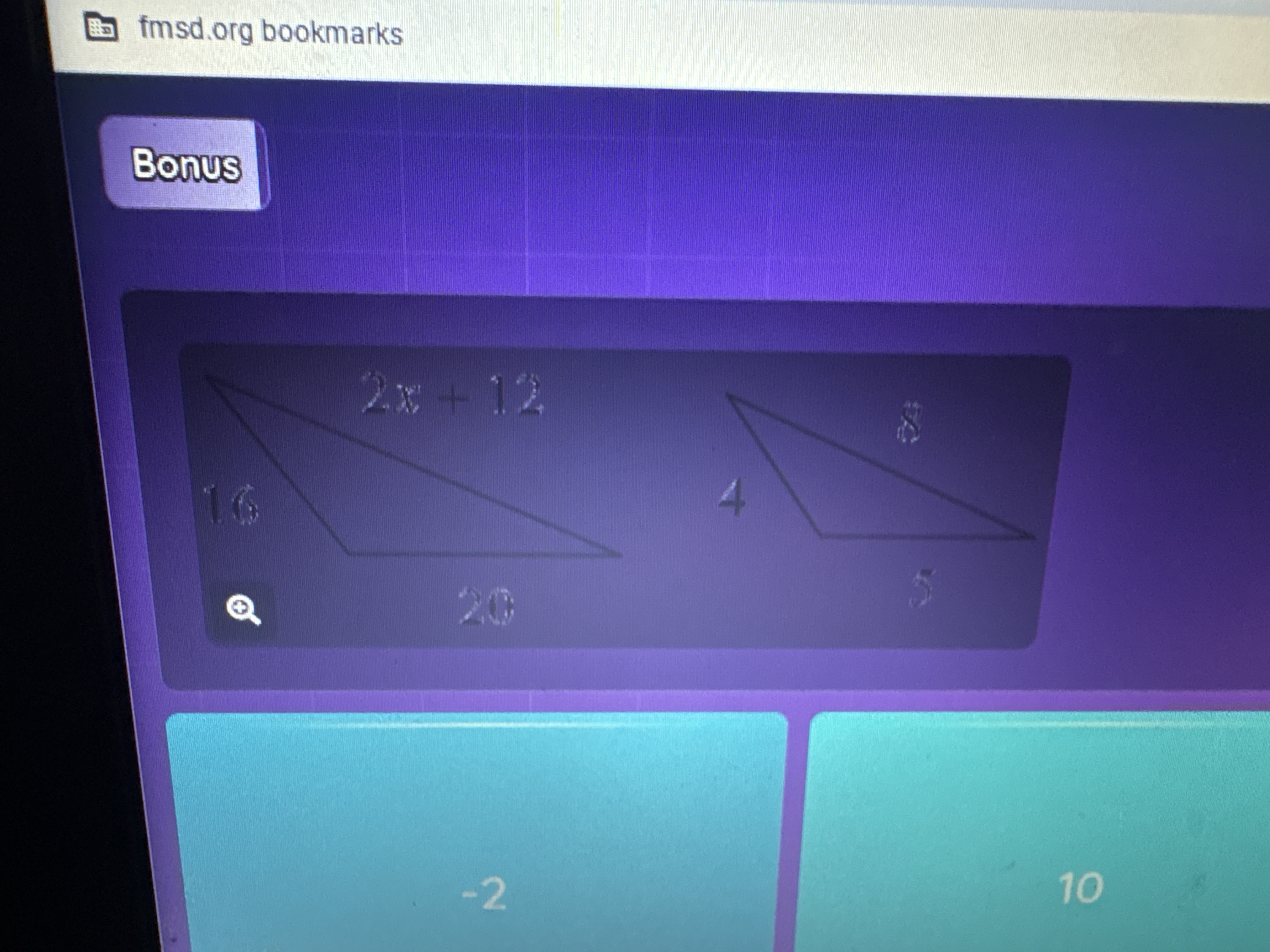
Solve for x in the equations related to the triangle measurements: 2x + 12, 16, and 20.
Understand the Problem
The question involves solving for the value of 'x' in a geometric context involving two triangles, where the sides of one triangle are represented with algebraic expressions. The user needs to apply the principles of geometry and algebra to find 'x'.
Answer
The value of $x$ is $10$.
Answer for screen readers
The value of $x$ is $10$.
Steps to Solve
- Identify the triangles and their dimensions
We have two triangles. The first triangle has dimensions:
- Height = 16
- Base = 20
- Side = $2x + 12$
The second triangle has dimensions:
- Height = 4
- Base = 5
- Side = 8
- Set up a proportion
Since the triangles are similar, we can set up proportions using corresponding sides. The ratio of the sides of the first triangle to the second triangle can be written as:
$$ \frac{2x + 12}{8} = \frac{20}{5} $$
- Simplify the proportion
Calculating the right side gives:
$$ \frac{20}{5} = 4 $$
So the proportion becomes:
$$ \frac{2x + 12}{8} = 4 $$
- Cross-multiply
To eliminate the fraction, cross-multiply:
$$ 2x + 12 = 4 \cdot 8 $$
Calculating the right side:
$$ 2x + 12 = 32 $$
- Solve for x
Subtract 12 from both sides:
$$ 2x = 32 - 12 $$
$$ 2x = 20 $$
Now, divide by 2:
$$ x = 10 $$
The value of $x$ is $10$.
More Information
The triangles' similarity allows the use of proportions to find the length of a side in one triangle based on the corresponding side lengths in the other triangle. Finding such dimensions is crucial in applications of geometry.
Tips
- Not recognizing the similarity between triangles, which can lead to incorrect proportions.
- Miscalculating during cross-multiplication or while simplifying equations.
AI-generated content may contain errors. Please verify critical information