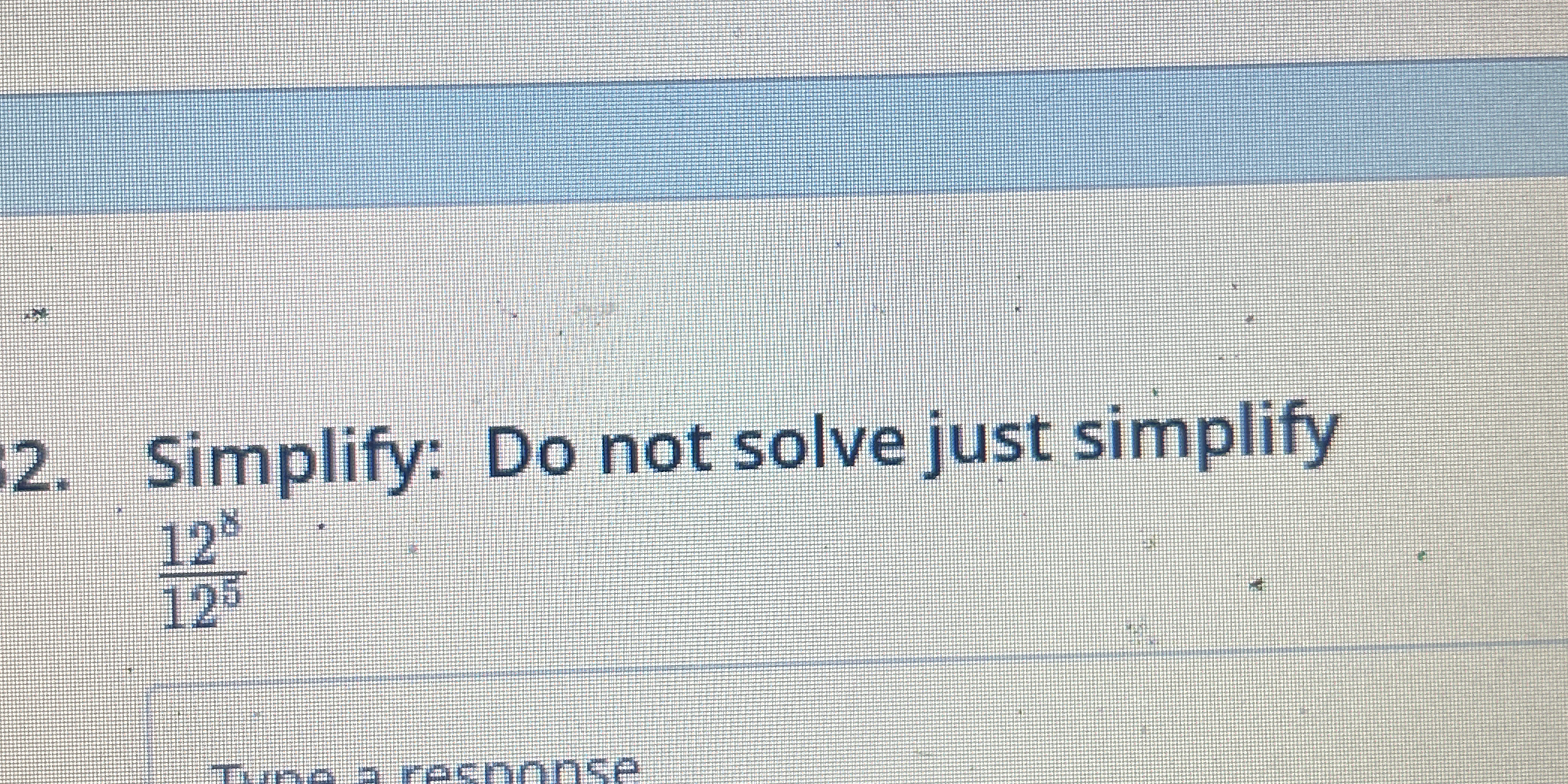
Simplify: Do not solve just simplify 12^b / 12^6
Understand the Problem
The question is asking to simplify the expression ( \frac{12^b}{12^6} ) without actually solving it.
Answer
The simplified expression is \( 12^{b - 6} \).
Answer for screen readers
The simplified expression is ( 12^{b - 6} ).
Steps to Solve
- Using the Quotient of Powers Rule
To simplify the expression ( \frac{12^b}{12^6} ), we apply the quotient of powers rule, which states that for any base ( a ) and exponents ( m ) and ( n ):
$$ \frac{a^m}{a^n} = a^{m-n} $$
Here, our base ( a ) is 12, ( m ) is ( b ), and ( n ) is 6.
- Applying the Rule
Using the quotient of powers rule, we rewrite the expression as:
$$ \frac{12^b}{12^6} = 12^{b - 6} $$
- Final Simplified Expression
The simplified form of the expression is:
$$ 12^{b - 6} $$
The simplified expression is ( 12^{b - 6} ).
More Information
This expression demonstrates the property of exponents which allows us to simplify expressions involving division of powers with the same base. This is useful in various fields of mathematics and applications, such as algebra and calculus.
Tips
- Neglecting the base: Forgetting to apply the base to both exponents during simplification.
- Incorrect subtraction: Miscalculating ( b - 6 ) when simplifying.
AI-generated content may contain errors. Please verify critical information