Simplify $5(\sqrt{\frac{7}{5}})^3$
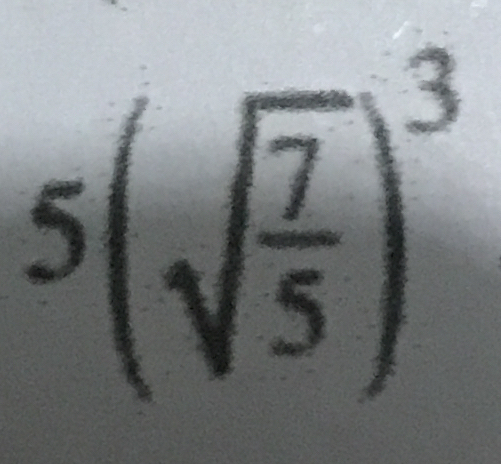
Understand the Problem
The question requires the simplification of a mathematical expression. The expression involves a number multiplied by a square root of a fraction, all raised to the power of 3. To solve, we need to simplify the expression, this will likely include rationalizing the denominator and dealing with the exponent.
Answer
$\frac{7\sqrt{35}}{5}$
Answer for screen readers
$\frac{7\sqrt{35}}{5}$
Steps to Solve
-
Rewrite the expression Rewrite the square root as a fractional exponent: $5(\sqrt{\frac{7}{5}})^3 = 5(\frac{7}{5})^{\frac{3}{2}}$
-
Distribute the exponent Apply the exponent to both the numerator and the denominator: $5(\frac{7}{5})^{\frac{3}{2}} = 5\frac{7^{\frac{3}{2}}}{5^{\frac{3}{2}}}$
-
Simplify the expression Rewrite $5$ as $5^1$ and combine the powers of 5: $5\frac{7^{\frac{3}{2}}}{5^{\frac{3}{2}}} = \frac{5^1 \cdot 7^{\frac{3}{2}}}{5^{\frac{3}{2}}} = \frac{7^{\frac{3}{2}}}{5^{\frac{1}{2}}}$
-
Rationalize the denominator Multiply the numerator and denominator by $5^{\frac{1}{2}}$ (which is the same as $\sqrt{5}$): $\frac{7^{\frac{3}{2}}}{5^{\frac{1}{2}}} \cdot \frac{5^{\frac{1}{2}}}{5^{\frac{1}{2}}} = \frac{7^{\frac{3}{2}} \cdot 5^{\frac{1}{2}}}{5}$
-
Rewrite in radical form Rewrite the fractional exponents as radicals: $\frac{7^{\frac{3}{2}} \cdot 5^{\frac{1}{2}}}{5} = \frac{7\sqrt{7}\sqrt{5}}{5} = \frac{7\sqrt{35}}{5}$
$\frac{7\sqrt{35}}{5}$
More Information
The simplified form of the expression $5(\sqrt{\frac{7}{5}})^3$ is $\frac{7\sqrt{35}}{5}$.
Tips
A common mistake is incorrectly applying the exponent to only the numerator or denominator inside the parenthesis, instead of applying it to the entire fraction. Also, students may forget to rationalize the denominator, leaving a square root in the denominator.
AI-generated content may contain errors. Please verify critical information