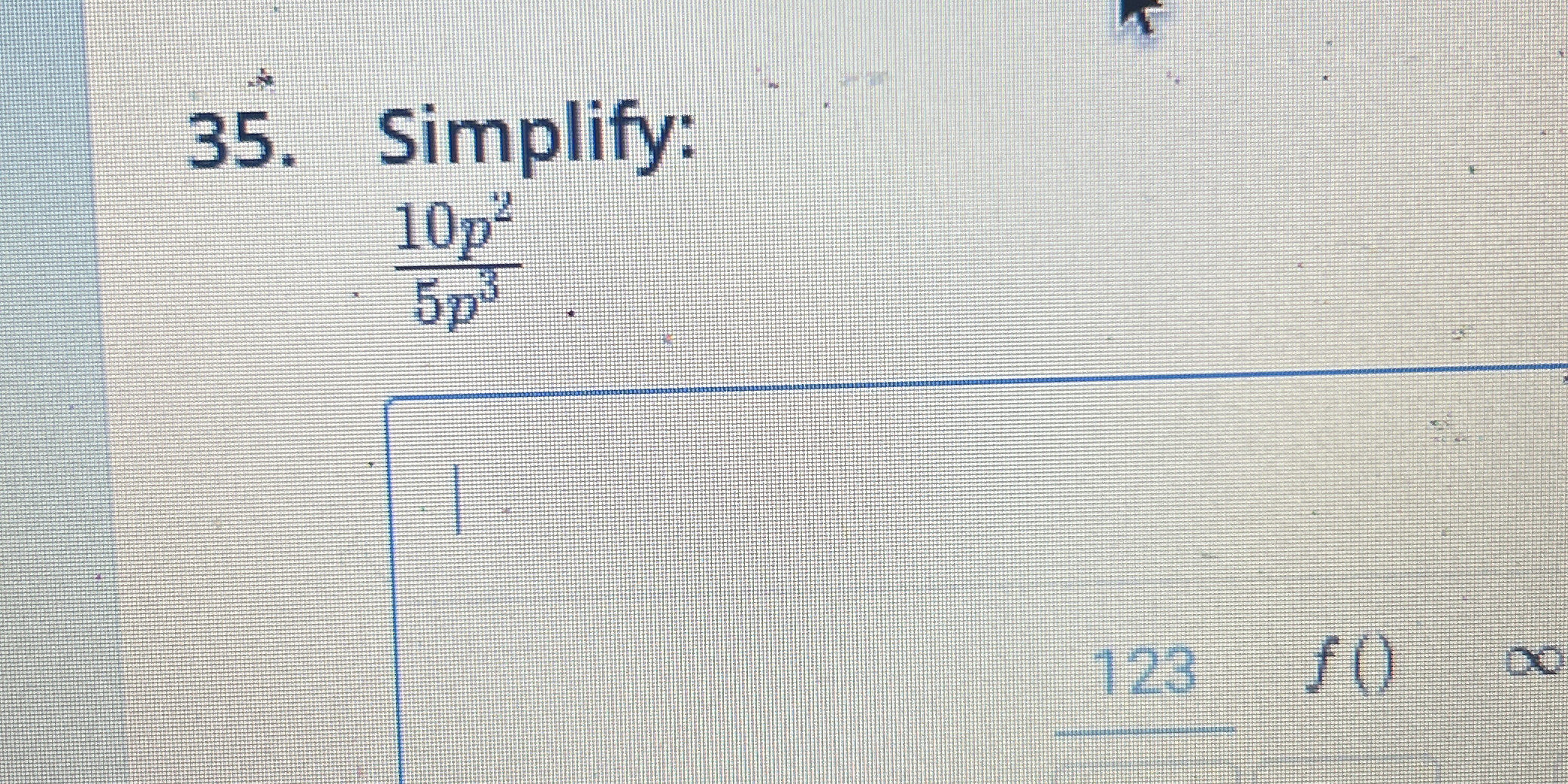
Simplify: 10p² / 5p³
Understand the Problem
The question is asking to simplify the expression 10p² / 5p³. This involves algebraic simplification where we can reduce the coefficients and subtract the powers of p.
Answer
The simplified expression is $\frac{2}{p}$.
Answer for screen readers
The simplified expression is:
$$ \frac{2}{p} $$
Steps to Solve
- Simplifying the Coefficients To simplify the expression, begin by dividing the coefficients. The expression can be rewritten as follows:
$$ \frac{10}{5} $$
Calculating that gives:
$$ 2 $$
- Simplifying the Variable Part Next, simplify the variable part $p^2$ and $p^3$. We apply the rule of exponents, which states that:
$$ \frac{p^a}{p^b} = p^{a-b} $$
In this case:
$$ \frac{p^2}{p^3} = p^{2-3} = p^{-1} $$
- Combining the Results Now we combine the results from both steps. We have:
$$ 2 \cdot p^{-1} $$
This can also be written as:
$$ \frac{2}{p} $$
The simplified expression is:
$$ \frac{2}{p} $$
More Information
This simplification shows how to reduce a fraction that involves both numerical coefficients and variables with exponents. It's a common technique in algebra to simplify expressions for easier calculations.
Tips
- Forgetting to apply the exponent rule correctly. Always remember that when dividing like bases, you subtract the exponents.
- Not simplifying the coefficients correctly. Ensure that both the numerator and denominator are divided properly.
AI-generated content may contain errors. Please verify critical information