Simplify: 1. 8x^2 / 12x^4; 2. 24x^2y / 32xy^3; 3. (x + 1)^3 / (x + 1)^5; 4. (3x - 2)^6 / (3x - 2)^4; 5. (2n - 3) / (3 - 2n); 6. 15y^2(y + 3) / 20y^3(y + 3); 7. 15y(y + 1) / 45y^2(y... Simplify: 1. 8x^2 / 12x^4; 2. 24x^2y / 32xy^3; 3. (x + 1)^3 / (x + 1)^5; 4. (3x - 2)^6 / (3x - 2)^4; 5. (2n - 3) / (3 - 2n); 6. 15y^2(y + 3) / 20y^3(y + 3); 7. 15y(y + 1) / 45y^2(y + 1); 8. 24x^3(4 - x) / 18x(4 - x); 9. 6x^3(2 - x) / 12x(2 - x); 10. 12x^3(5 - 2x) / 18x(2 - 5); 11. a^2 + 6a / ac + 6c; 12. x^2 + 4x / 3x + 12; 13. 6 - 8x / 4x^2 - 3x; 14. x^2 + 2x - 15 / x^2 - 10x + 21; 15. x^2 - 2x - 3 / x^2 - 5x - 6
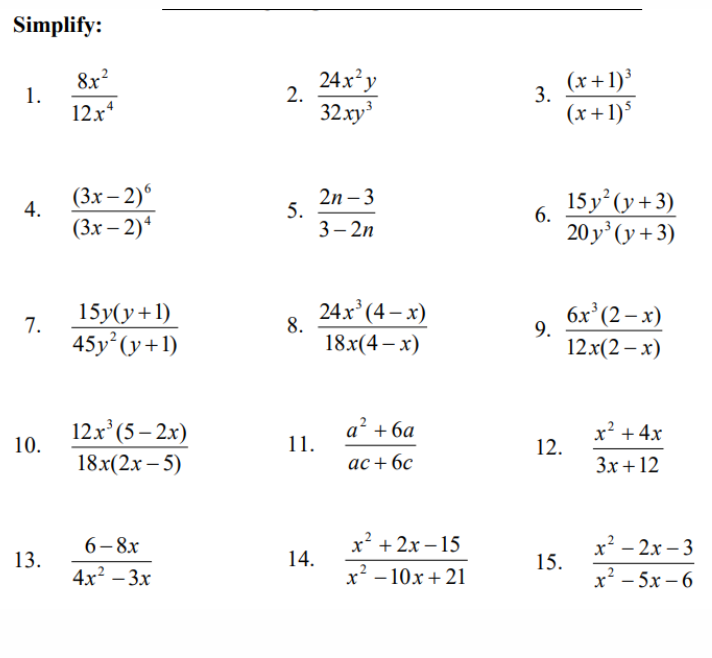
Understand the Problem
The question is asking to simplify various algebraic expressions. This involves performing operations such as factoring, canceling terms, and reducing fractions where possible.
Answer
Answer for screen readers
Steps to Solve
-
Simplifying Expression 1: Start with the expression $$ \frac{8x^2}{12x^4} $$ Factor out the greatest common divisor (GCD), which is 4: $$ \frac{8x^2 \div 4}{12x^4 \div 4} = \frac{2x^2}{3x^4} $$ Now, simplify the powers of $x$: $$ \frac{2}{3} \cdot \frac{x^2}{x^4} = \frac{2}{3} \cdot \frac{1}{x^{4-2}} = \frac{2}{3x^2} $$
-
Simplifying Expression 2: Start with $$ \frac{24x^2y}{32xy^3} $$ The GCD is 8: $$ \frac{24x^2y \div 8}{32xy^3 \div 8} = \frac{3x^2y}{4xy^3} $$ Next, simplify: $$ \frac{3}{4} \cdot \frac{x^2}{x} \cdot \frac{y}{y^3} = \frac{3}{4} \cdot x^{2-1} \cdot y^{1-3} = \frac{3x}{4y^2} $$
-
Simplifying Expression 3: Start with $$ \frac{(x+1)^3}{(x+1)^5} $$ Simplifying the powers: $$ (x+1)^{3-5} = (x+1)^{-2} = \frac{1}{(x+1)^2} $$
-
Simplifying Expression 4: Start with $$ \frac{(3x-2)^6}{(3x-2)^4} $$ Simplifying the powers: $$ (3x-2)^{6-4} = (3x-2)^2 $$
-
Simplifying Expression 5: Start with $$ \frac{2n - 3}{3 - 2n} $$ Factor out -1 from the denominator: $$ \frac{2n - 3}{-(2n - 3)} = -1 $$
-
Simplifying Expression 6: Start with $$ \frac{15y^2(y + 3)}{20y^3(y + 3)} $$ Cancel the common term $(y + 3)$: $$ \frac{15y^2}{20y^3} $$ GCD is 5: $$ \frac{15 \div 5}{20 \div 5} \cdot \frac{y^2}{y^3} = \frac{3}{4} \cdot \frac{1}{y} = \frac{3}{4y} $$
-
Simplifying Expression 7: Start with $$ \frac{15y(y + 1)}{45y^2(y + 1)} $$ Cancel $(y + 1)$: $$ \frac{15y}{45y^2} $$ GCD is 15: $$ \frac{15 \div 15}{45 \div 15} \cdot \frac{1}{y} = \frac{1}{3y} $$
-
Simplifying Expression 8: Start with $$ \frac{24x^3(4 - x)}{18x(4 - x)} $$ Cancel $(4 - x)$: $$ \frac{24x^3}{18x} $$ GCD is 6: $$ \frac{24 \div 6}{18 \div 6} \cdot x^{3-1} = \frac{4}{3} \cdot x^2 = \frac{4x^2}{3} $$
-
Simplifying Expression 9: Start with $$ \frac{6x^3(2 - x)}{12x(2 - x)} $$ Cancel $(2 - x)$: $$ \frac{6x^3}{12x} $$ GCD is 6: $$ \frac{6 \div 6}{12 \div 6} \cdot x^{3-1} = \frac{1}{2} \cdot x
AI-generated content may contain errors. Please verify critical information