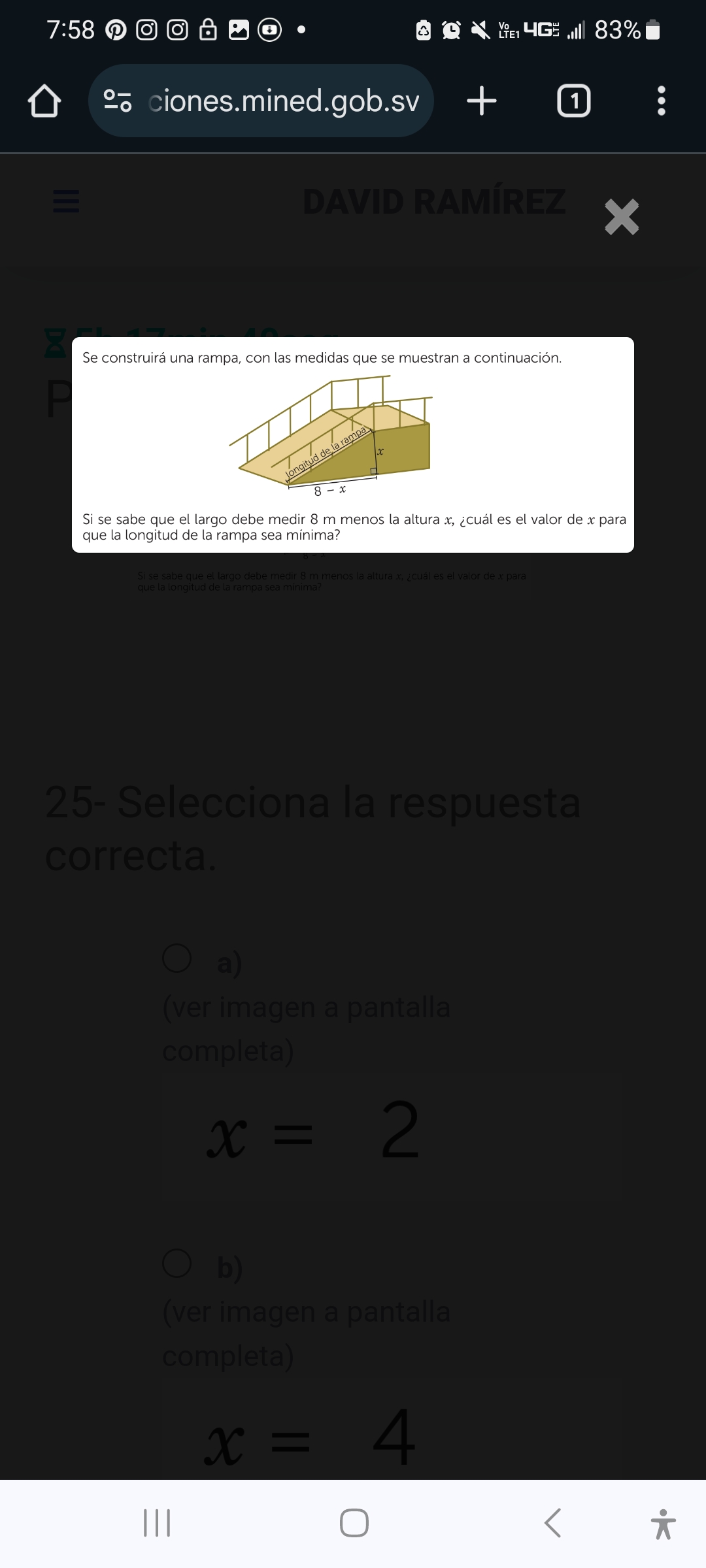
Si se sabe que el largo debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la rampa sea mínima?

Understand the Problem

El problema plantea una rampa donde la longitud de la base es 8 metros menos la altura (x). Se pide encontrar el valor de x (la altura) que hará que la longitud de la rampa sea mínima. Esto implica usar el teorema de Pitágoras para expresar la longitud de la rampa en función de x, y luego encontrar el valor de x que minimiza esta expresión.

Answer

$x = 4$

Steps to Solve

Define the length of the ramp using the Pythagorean theorem

Let $L$ be the length of the ramp. According to the Pythagorean theorem, we have:

$$L^2 = x^2 + (8-x)^2$$

Express $L^2$ as a function of $x$

Expanding the equation:

$$L^2 = x^2 + (64 - 16x + x^2)$$

$$L^2 = 2x^2 - 16x + 64$$ Let $f(x) = 2x^2 - 16x + 64$. We want to minimize this function.

Find the critical points

To find the minimum length of the ramp, we need to find the critical points of the function $f(x)$. We can do this by taking the derivative of $f(x)$ with respect to $x$ and setting it equal to 0:

$$f'(x) = 4x - 16$$

Setting $f'(x) = 0$:

$$4x - 16 = 0$$

$$4x = 16$$

$$x = 4$$

Verify that it's a minimum

To ensure that $x = 4$ corresponds to a minimum, we can perform the second derivative test. Taking the second derivative of $f(x)$:

$$f''(x) = 4$$

Since $f''(x) = 4 > 0$, the function $f(x)$ has a minimum at $x = 4$.

$x = 4$

More Information

The height $x$ that minimizes the length of the ramp is 4 meters.

Tips

A common mistake is to only find the first derivative and set it to zero, but forget to check if it's a minimum or a maximum using the second derivative test (or by analyzing the sign of the first derivative around the critical point). Failing to expand the $(8-x)^2$ term correctly when applying the Pythagorean theorem is another possible mistake.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!