Given that \(A = \begin{pmatrix} 3 & 1 \\ 2 & 0 \end{pmatrix}\), \(X = \begin{pmatrix} 5 & 1 \\ 4 & 1 \end{pmatrix}\), and \(Z = \begin{pmatrix} 2 & 0 \\ 3 & 3 \end{pmatrix}\), fin... Given that \(A = \begin{pmatrix} 3 & 1 \\ 2 & 0 \end{pmatrix}\), \(X = \begin{pmatrix} 5 & 1 \\ 4 & 1 \end{pmatrix}\), and \(Z = \begin{pmatrix} 2 & 0 \\ 3 & 3 \end{pmatrix}\), find \(A(X-Z)^2 + X\).
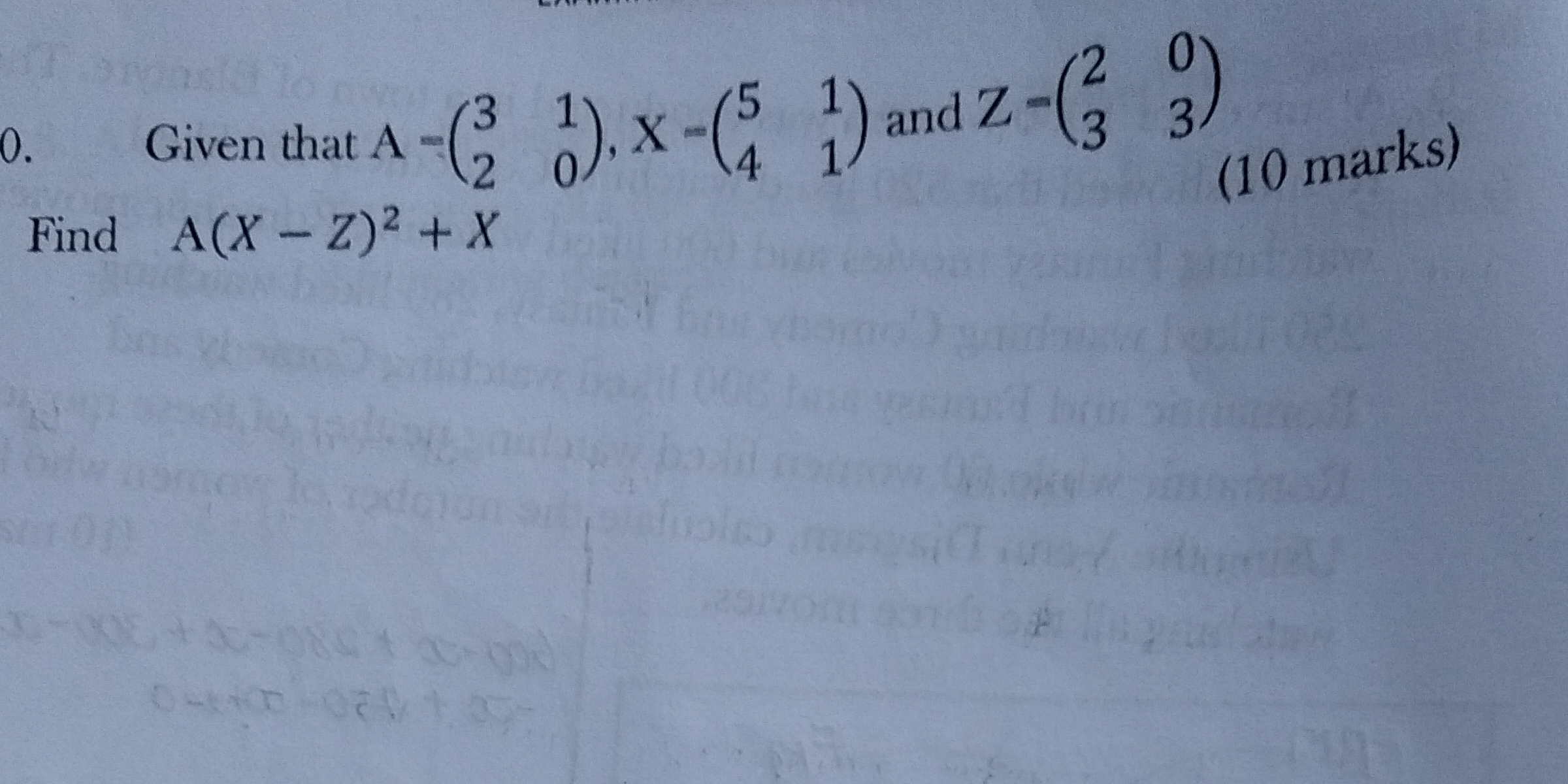
Understand the Problem
The question asks to find (A(X-Z)^2 + X) given the matrices (A), (X), and (Z). First, the difference (X-Z) must be found, then square the resulting matrix, before pre-multiplying by (A) and adding (X) at the end.
Answer
$\begin{pmatrix} 36 & 9 \\ 24 & 3 \end{pmatrix}$
Answer for screen readers
$A(X-Z)^2 + X = \begin{pmatrix} 36 & 9 \ 24 & 3 \end{pmatrix}$
Steps to Solve
- Calculate $X - Z$
To find $X - Z$, subtract the corresponding entries of matrix $Z$ from matrix $X$: $$ X - Z = \begin{pmatrix} 5 & 1 \ 4 & 1 \end{pmatrix} - \begin{pmatrix} 2 & 0 \ 3 & 3 \end{pmatrix} = \begin{pmatrix} 5-2 & 1-0 \ 4-3 & 1-3 \end{pmatrix} = \begin{pmatrix} 3 & 1 \ 1 & -2 \end{pmatrix} $$
- Calculate $(X - Z)^2$
To find $(X - Z)^2$, multiply the matrix $(X - Z)$ by itself: $$ (X - Z)^2 = \begin{pmatrix} 3 & 1 \ 1 & -2 \end{pmatrix} \begin{pmatrix} 3 & 1 \ 1 & -2 \end{pmatrix} = \begin{pmatrix} (3\times3 + 1\times1) & (3\times1 + 1\times-2) \ (1\times3 + -2\times1) & (1\times1 + -2\times-2) \end{pmatrix} = \begin{pmatrix} 9+1 & 3-2 \ 3-2 & 1+4 \end{pmatrix} = \begin{pmatrix} 10 & 1 \ 1 & 5 \end{pmatrix} $$
- Calculate $A(X - Z)^2$
To find $A(X - Z)^2$, multiply matrix $A$ by $(X - Z)^2$: $$ A(X - Z)^2 = \begin{pmatrix} 3 & 1 \ 2 & 0 \end{pmatrix} \begin{pmatrix} 10 & 1 \ 1 & 5 \end{pmatrix} = \begin{pmatrix} (3\times10 + 1\times1) & (3\times1 + 1\times5) \ (2\times10 + 0\times1) & (2\times1 + 0\times5) \end{pmatrix} = \begin{pmatrix} 30+1 & 3+5 \ 20+0 & 2+0 \end{pmatrix} = \begin{pmatrix} 31 & 8 \ 20 & 2 \end{pmatrix} $$
- Calculate $A(X - Z)^2 + X$
To find $A(X - Z)^2 + X$, add matrix $X$ to the result from the previous step: $$ A(X - Z)^2 + X = \begin{pmatrix} 31 & 8 \ 20 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 1 \ 4 & 1 \end{pmatrix} = \begin{pmatrix} 31+5 & 8+1 \ 20+4 & 2+1 \end{pmatrix} = \begin{pmatrix} 36 & 9 \ 24 & 3 \end{pmatrix} $$
$A(X-Z)^2 + X = \begin{pmatrix} 36 & 9 \ 24 & 3 \end{pmatrix}$
More Information
Matrix operations such as addition, subtraction, and multiplication are fundamental in linear algebra. Matrix multiplication is not commutative, so the order of multiplication matters.
Tips
A common mistake is to square each element of the matrix $(X-Z)$ individually instead of performing matrix multiplication. Another common mistake is to mix up the order of matrix multiplication, as matrix multiplication is not commutative.
AI-generated content may contain errors. Please verify critical information