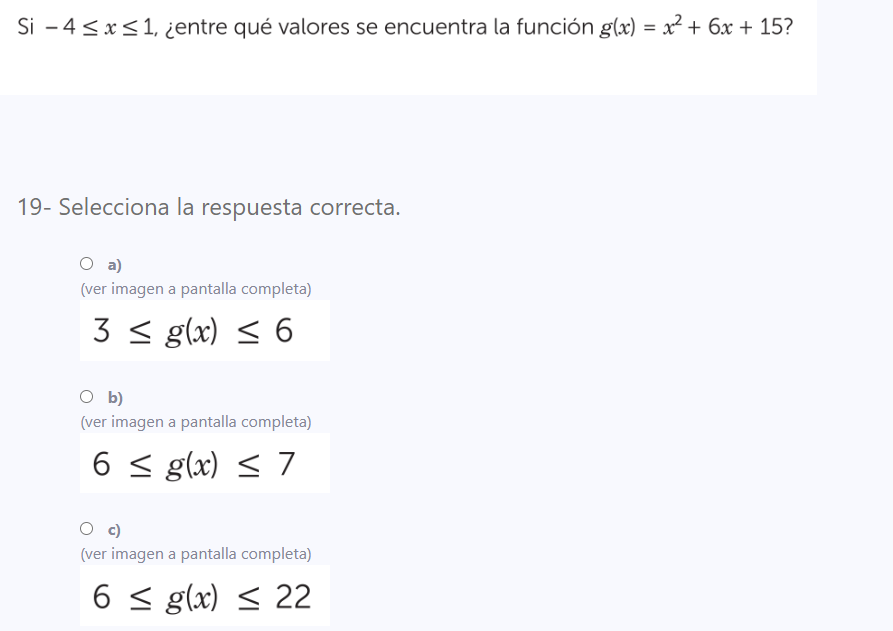
Si -4 ≤ x ≤ 1, ¿entre qué valores se encuentra la función g(x) = x² + 6x + 15?
Understand the Problem
La pregunta está pidiendo determinar los valores entre los cuales se encuentra la función g(x) = x² + 6x + 15, dado el intervalo de -4 ≤ x ≤ 1. Se deben evaluar los extremos del intervalo en la función para encontrar el rango correspondiente.
Answer
$7 \leq g(x) \leq 22$
Answer for screen readers
El rango de la función es $7 \leq g(x) \leq 22$.
Steps to Solve
-
Evaluar los extremos del intervalo
Primero, evaluamos la función $g(x) = x^2 + 6x + 15$ en los extremos del intervalo $x = -4$ y $x = 1$.
-
Calcular $g(-4)$
Sustituyendo $x = -4$ en la función:
$$ g(-4) = (-4)^2 + 6(-4) + 15 $$ $$ g(-4) = 16 - 24 + 15 $$ $$ g(-4) = 7 $$
-
Calcular $g(1)$
Ahora sustituimos $x = 1$ en la función:
$$ g(1) = (1)^2 + 6(1) + 15 $$ $$ g(1) = 1 + 6 + 15 $$ $$ g(1) = 22 $$
-
Determinar el rango
Con los valores calculados, vemos que $g(x)$ varía de $g(-4) = 7$ hasta $g(1) = 22$. Por lo tanto, el rango en el intervalo $-4 \leq x \leq 1$ es:
$$ 7 \leq g(x) \leq 22 $$
El rango de la función es $7 \leq g(x) \leq 22$.
More Information
La función dada es un trinomio cuadrático que representa una parábola. Dado que estamos evaluando en un intervalo cerrado, los valores extremos se encuentran efectivamente al calcular la función en los puntos extremos del intervalo.
Tips
- Olvidar evaluar en ambos extremos: Asegúrate de calcular el valor de la función en todos los extremos del intervalo.
- No considerar el tipo de función: Recordar que la parábola abre hacia arriba en este caso, lo que significa que los extremos evaluados son importantes para determinar el rango.
AI-generated content may contain errors. Please verify critical information