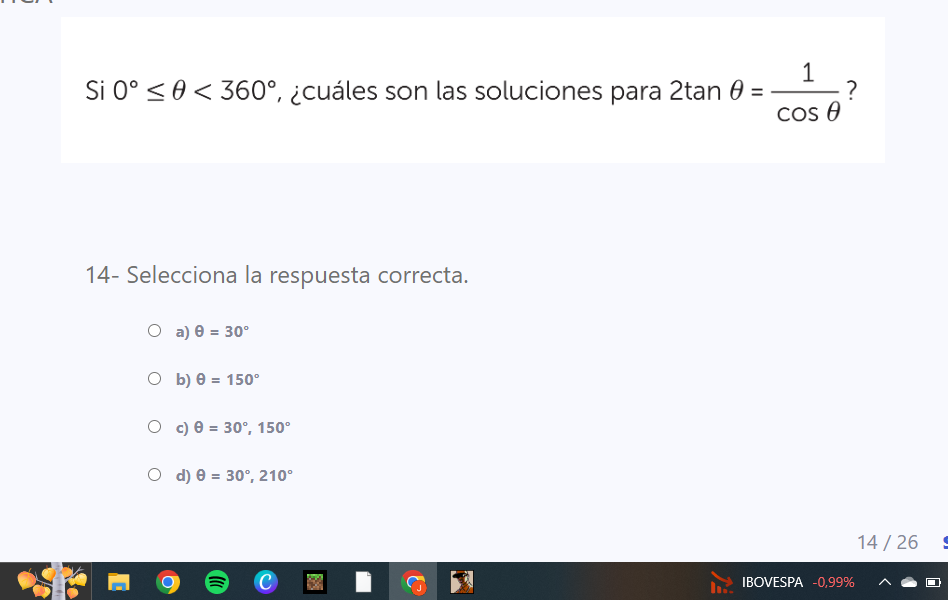
Si 0° ≤ θ < 360°, ¿cuáles son las soluciones para 2tan(θ) = -1/cos(θ)?
Understand the Problem
La pregunta está pidiendo las soluciones para el ángulo θ en el intervalo de 0° a 360° que satisfacen la ecuación dada, 2tan(θ) = -1/cos(θ). Es necesario resolver la ecuación y determinar los valores de θ que cumplen con esta condición.
Answer
Las soluciones son $\theta = 210°, 330°$.
Answer for screen readers
Las soluciones para la ecuación $2\tan(\theta) = -\frac{1}{\cos(\theta)}$ en el intervalo $0° \leq \theta < 360°$ son $\theta = 210°, 330°$.
Steps to Solve
-
Reescribir la ecuación La ecuación dada es $2\tan(\theta) = -\frac{1}{\cos(\theta)}$. Podemos reescribirla utilizando la relación $\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$. Esto nos da: $$ 2\frac{\sin(\theta)}{\cos(\theta)} = -\frac{1}{\cos(\theta)} $$
-
Multiplicar por coseno Multiplicamos ambos lados de la ecuación por $\cos(\theta)$ para eliminar el denominador: $$ 2\sin(\theta) = -1 $$
-
Resolver para sen(θ) Despejamos $\sin(\theta)$: $$ \sin(\theta) = -\frac{1}{2} $$
-
Encontrar ángulos que satisfacen la función seno Buscamos en el círculo unitario los ángulos donde $\sin(\theta) = -\frac{1}{2}$. Esto ocurre en:
- El cuarto cuadrante: $\theta = 330°$
- El tercer cuadrante: $\theta = 210°$
- Comprobar las soluciones Comprobamos que ambos ángulos cumplen con la condición original de la ecuación.
Las soluciones para la ecuación $2\tan(\theta) = -\frac{1}{\cos(\theta)}$ en el intervalo $0° \leq \theta < 360°$ son $\theta = 210°, 330°$.
More Information
La función seno es negativa en los cuadrantes tercero y cuarto. Esta propiedad se utiliza para encontrar las soluciones, además es importante recordar las relaciones trigonométricas y su dominio.
Tips
- Olvidar el signo: Asegúrate de tener en cuenta el signo negativo al resolver para $\sin(\theta)$.
- No considerar todos los cuadrantes: A veces, los estudiantes solo consideran un cuadrante, pero necesitamos buscar en todos los que cumplen la condición.
AI-generated content may contain errors. Please verify critical information