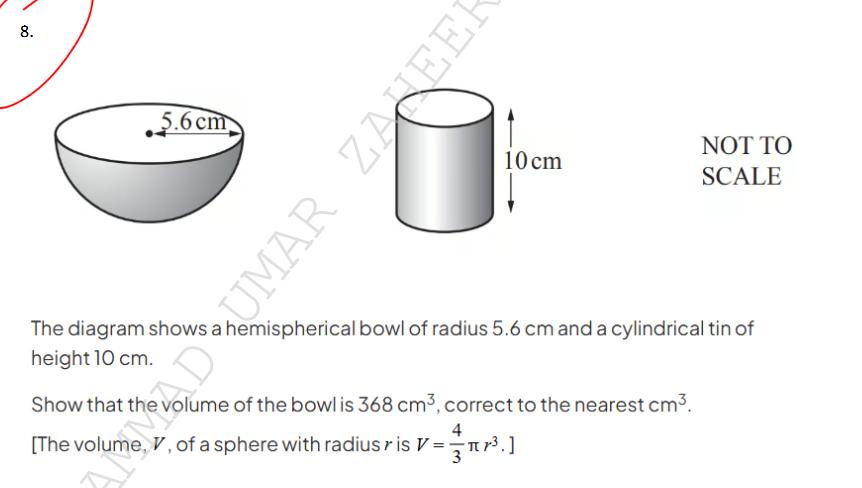
Show that the volume of the bowl is 368 cm³, correct to the nearest cm³.

Steps to Solve

1. Understand the formula for a sphere's volume

The volume ( V ) of a sphere with radius ( r ) is given by the formula: $$ V = \frac{4}{3} \pi r^3 $$

2. Adapt the formula for a hemisphere

The volume of a hemisphere is half the volume of a sphere. Thus, to find the volume of the bowl: $$ V_{\text{hemisphere}} = \frac{1}{2} \times \frac{4}{3} \pi r^3 $$

3. Substitute the radius into the equation

Given that the radius ( r = 5.6 ) cm, we can substitute this value into the formula: $$ V_{\text{hemisphere}} = \frac{1}{2} \times \frac{4}{3} \pi (5.6)^3 $$

4. Calculate ( (5.6)^3 )

First, calculate ( (5.6)^3 ): $$ (5.6)^3 = 5.6 \times 5.6 \times 5.6 = 175.616 $$

5. Calculate the volume

Now substitute this value back into the volume formula: $$ V_{\text{hemisphere}} = \frac{1}{2} \times \frac{4}{3} \pi (175.616) $$ This simplifies to: $$ V_{\text{hemisphere}} = \frac{2}{3} \pi (175.616) $$

6. Use ( \pi \approx 3.14 ) for calculations

Approximate ( \pi ) as 3.14 for calculation: $$ V_{\text{hemisphere}} \approx \frac{2}{3} \times 3.14 \times 175.616 $$

7. Final calculation

Now calculate the final volume: $$ V_{\text{hemisphere}} \approx \frac{2 \times 3.14 \times 175.616}{3} $$ Calculate: $$ V \approx \frac{1101.64672}{3} \approx 367.21557 $$

8. Round to the nearest cm³

Finally, round the result to the nearest cm³: $$ V \approx 368 \text{ cm}^3 $$