Show that the matrix A = [[3, 7+4i, -2+5i], [7-4i, -2, 3+i], [-2-5i, 3-i, 4]] is a Hermitian matrix.
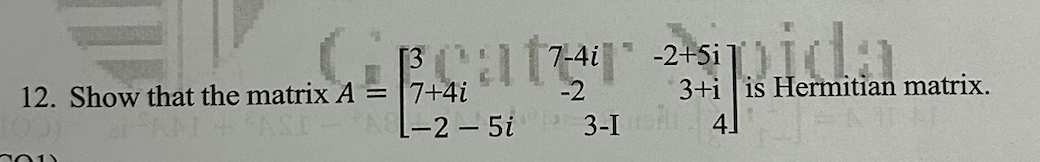
Understand the Problem
The question is asking to demonstrate that a given matrix is a Hermitian matrix. This involves checking if the matrix is equal to its conjugate transpose.
Answer
The matrix \( A \) is Hermitian, as \( A = A^* \).
Answer for screen readers
The matrix ( A ) is a Hermitian matrix, as it satisfies ( A = A^* ).
Steps to Solve
- Write down the matrix ( A )
We have the matrix ( A ): $$ A = \begin{bmatrix} 3 & 7 + 4i & -2 + 5i \ 7 - 4i & -2 & 3 + i \ -2 - 5i & 3 - i & 4 \end{bmatrix} $$
- Calculate the conjugate transpose ( A^ )*
The conjugate transpose ( A^* ) is found by taking the transpose of the matrix and then taking the complex conjugate of each element.
The transpose of ( A ) is: $$ A^T = \begin{bmatrix} 3 & 7 - 4i & -2 - 5i \ 7 + 4i & -2 & 3 - i \ -2 + 5i & 3 + i & 4 \end{bmatrix} $$
Now we take the complex conjugate of each element: $$ A^* = \begin{bmatrix} 3 & 7 + 4i & -2 + 5i \ 7 - 4i & -2 & 3 + i \ -2 - 5i & 3 - i & 4 \end{bmatrix} $$
- Compare ( A ) and ( A^ )*
To show that ( A ) is Hermitian, we need to check if ( A = A^* ).
Looking at the matrix: $$ A = A^* = \begin{bmatrix} 3 & 7 + 4i & -2 + 5i \ 7 - 4i & -2 & 3 + i \ -2 - 5i & 3 - i & 4 \end{bmatrix} $$
Since all corresponding elements are equal, we conclude that ( A ) is Hermitian.
The matrix ( A ) is a Hermitian matrix, as it satisfies ( A = A^* ).
More Information
Hermitian matrices are important in quantum mechanics and many areas of symmetric operations because they have real eigenvalues and orthogonal eigenvectors. They also exhibit nice properties under operations such as addition and scalar multiplication.
Tips
- Forgetting to take the complex conjugate of the imaginary parts when finding the conjugate transpose of the matrix.
- Confusing the transpose and the conjugate transpose. Remember that the conjugate transpose involves both operations.