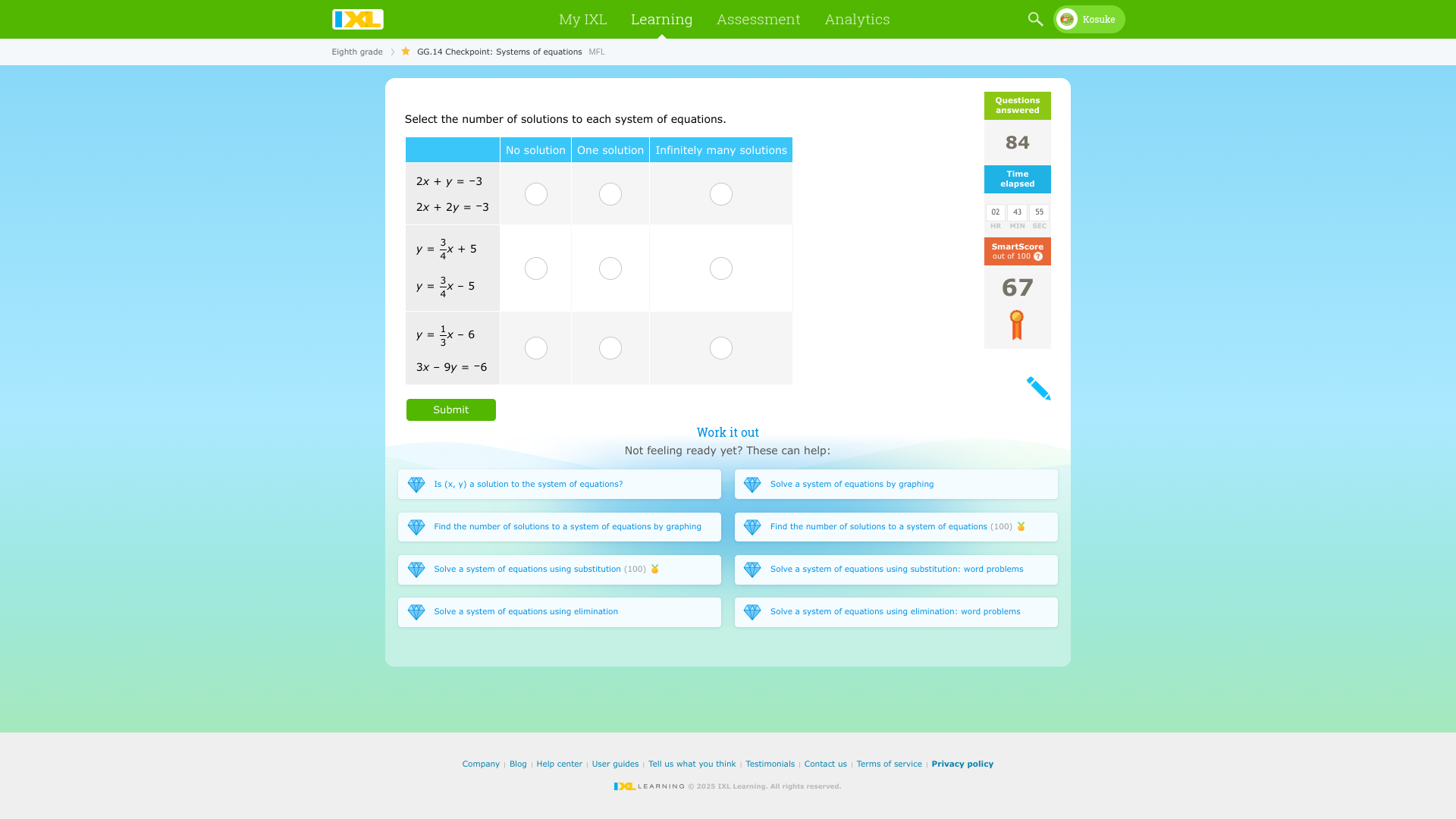
Select the number of solutions to each system of equations.
Understand the Problem
The question requires the user to determine the number of solutions for each system of equations presented. It is aiming to evaluate their understanding of systems of equations in algebra.
Answer
1. No solution 2. Infinitely many solutions 3. One solution 4. One solution
Answer for screen readers
- No solution
- Infinitely many solutions
- One solution
- One solution
Steps to Solve
-
Identify the systems of equations We need to analyze all four pairs of equations provided to determine the number of solutions.
-
Check for parallel lines (no solutions) For systems of equations, if the lines are parallel (same slope, different y-intercept), there are no solutions. We can identify this by rewriting each equation in slope-intercept form, $y = mx + b$ and comparing the slopes.
-
Check for overlapping lines (infinitely many solutions) If both equations simplify to the same line (identical equations), there are infinitely many solutions. Again, convert each equation to slope-intercept form.
-
Check for intersecting lines (one solution) If the lines intersect at a single point (different slopes), then there is one unique solution. Compare slopes to identify if they're different.
-
Analyze each set of equations:
- For $2x + y = -3$ and $2y = -3$: Both must be rewritten to compare slopes.
- For $y = \frac{3}{4}x + 5$ and $y = \frac{3}{4}x - 5$: Again, check slopes.
- For $y = \frac{1}{3}x - 6$ and $3x - 9y = -6$: Convert to slope-intercept form to compare.
- For $3x - 9y = -6$: Rewrite and analyze.
- No solution
- Infinitely many solutions
- One solution
- One solution
More Information
- The relationships between the equations help identify whether they intersect, are parallel, or overlap entirely, which determines the solution status.
- Systems of equations can be visualized graphically, making it easier to identify slopes and intercepts.
Tips
- Confusing parallel lines with intersecting lines; both have specific slopes but only intersecting lines solve to a unique point.
- Miscalculating the slope when converting to slope-intercept form. Always double-check calculations.
AI-generated content may contain errors. Please verify critical information