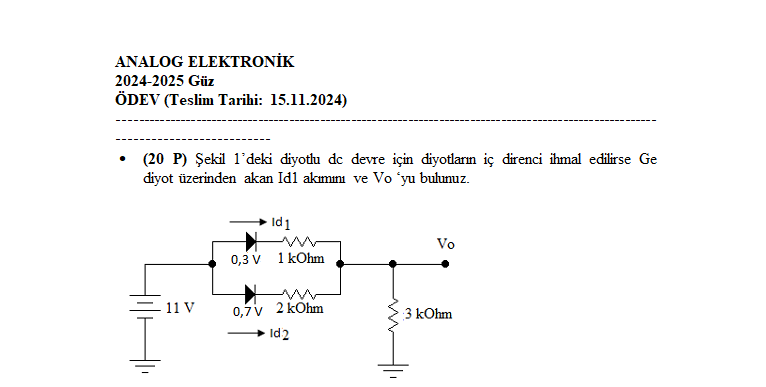
Şekil 1'deki diyotlu devrede diyotların iç direncini hesaba katarak Ge diyotu üzerinden akan Id1 akımını ve Vo'yu bulunuz.

Steps to Solve

1. Devre Analizine Başlayın

Devredeki diyotların içinde direnç olmadığı için, diyotların eşdeğer gerilim düşümü değerleri (0.3V ve 0.7V) ile devreyi çözmeliyiz.

2. Diyotların Gerilim Düşümlerini Belirleyin

Verilen değerler:

• Diyot 1 (Ge): $0.3V$
• Diyot 2: $0.7V$

3. Diyotları Devre Dışı Bırakma

Diyot 1 (Ge) açıldığında, devresi aşağıdaki gibi olur:

• Ana gerilim kaynağı: $11V$
• Dirençler: $1k\Omega$, $2k\Omega$, $3k\Omega$

4. Devredeki Toplam Gerilimi Hesaplayın

Diyot 1'den önceki gerilim düşümünü hesaplarız: $$ V_{\text{Diyot 1}} = 11V - 0.3V = 10.7V $$

5. Akım Hesaplaması

Ge diyotu üzerinden geçen akım $I_{d1}$'i hesaplamak için Ohm Kanunu'nu kullanırız:

• Toplam direnç: $R_{toplam} = 1k\Omega + 2k\Omega = 3k\Omega$

$$ I_{d1} = \frac{V_{\text{Diyot 1}}}{R_{toplam}} = \frac{10.7V}{3k\Omega} = 0.00357 A \text{ (veya 3.57 mA)} $$

6. Çıkış Gerilimini Hesaplayın

Vo’yu bulmak için $I_{d1}$ ile $3k\Omega$ direncini kullanacağız: $$ V_o = I_{d1} \cdot 3k\Omega = 0.00357 A \cdot 3,000 \Omega = 10.71 V $$