[(log_2(t) + log_2(b)] / [log_2(a) + log_2(c)]

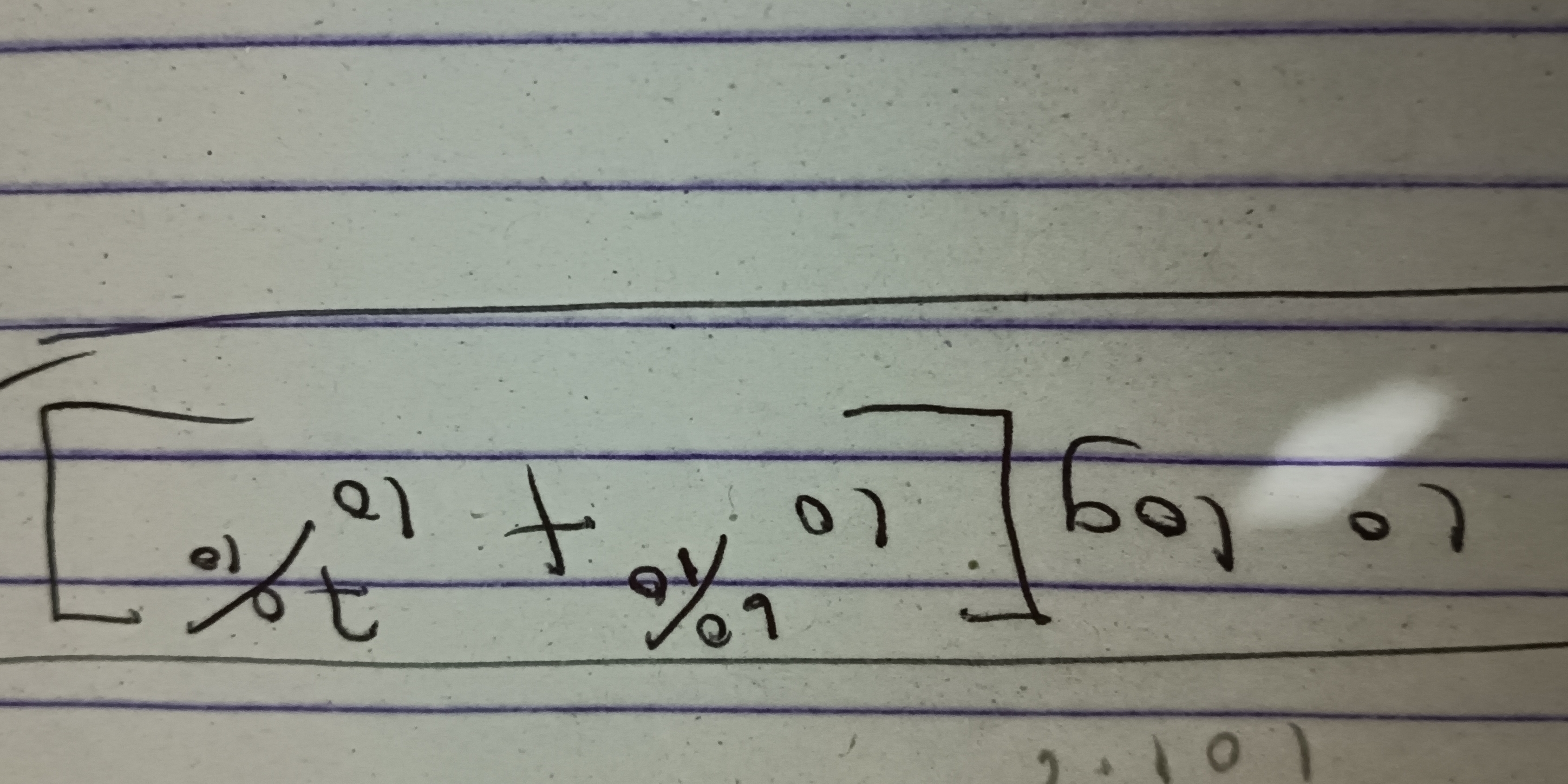
Understand the Problem

The question is asking us to solve or simplify a mathematical expression that involves logarithmic terms. It appears to consist of a fraction with logarithmic components, and we need to analyze and potentially simplify it step by step.

Answer

The expression simplifies to $ \log_{a \cdot c}(t \cdot b) $.

Steps to Solve

Combine the Logarithms in the Numerator

Using the property of logarithms that states $ \log_b(m) + \log_b(n) = \log_b(m \cdot n) $, we can combine the logarithms in the numerator:

$$ \log_2(t) + \log_2(b) = \log_2(t \cdot b) $$

So, the numerator becomes:

$$ \log_2(t \cdot b) $$

Combine the Logarithms in the Denominator

Similarly, we apply the same property for the denominator:

$$ \log_2(a) + \log_2(c) = \log_2(a \cdot c) $$

So, the denominator becomes:

$$ \log_2(a \cdot c) $$

Construct the Full Expression

Now, we can rewrite the entire expression:

$$ \frac{\log_2(t \cdot b)}{\log_2(a \cdot c)} $$

Use Another Property of Logarithms

If we apply the property that states $ \frac{\log_b(x)}{\log_b(y)} = \log_y(x) $, we can simplify the expression further:

$$ \log_{a \cdot c}(t \cdot b) $$

The simplified expression is:

$$ \log_{a \cdot c}(t \cdot b) $$

More Information

This result demonstrates the properties of logarithms, such as the addition of logarithms leading to multiplication and the conversion from one base to another. This technique is essential in simplifying logarithmic expressions in various fields, including mathematics and engineering.

Tips

Forgetting Logarithm Properties: Students may forget the properties of logarithms, such as combining logarithms using multiplication or division.
Incorrect Base Application: Mixing up the base of logarithms while simplifying can lead to incorrect results. Always check that you are applying the properties correctly based on the logarithm in question.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!