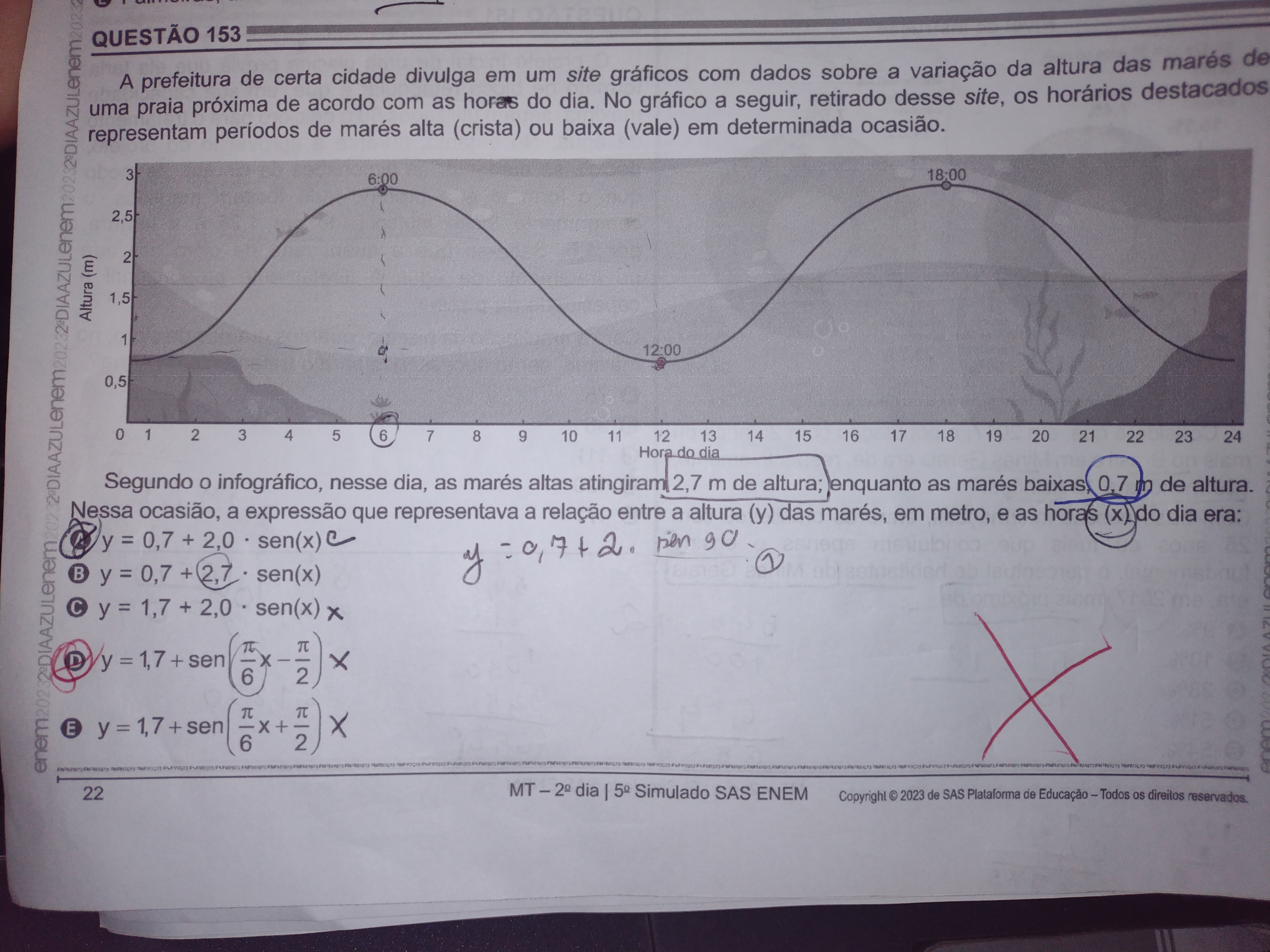
Segundo o infográfico, nesse dia, as marés altas atingem 2,7 m de altura, enquanto as marés baixas, 0,7 m de altura. A expressão que representava a relação entre a altura (y) das m... Segundo o infográfico, nesse dia, as marés altas atingem 2,7 m de altura, enquanto as marés baixas, 0,7 m de altura. A expressão que representava a relação entre a altura (y) das marés, em metro, e as horas (x) do dia era: Read more

Steps to Solve

1. Identificação da amplitude e altura média As marés altas atingem 2,7 m e as baixas atingem 0,7 m. A amplitude (a) é a diferença entre a altura máxima e a mínima, ou seja:

$$ a = \frac{2,7 - 0,7}{2} = 1 $$

A altura média (b) é dada pela média entre a máxima e a mínima:

$$ b = \frac{2,7 + 0,7}{2} = 1,7 $$

2. Escolha da função senoidal Como as marés são periódicas e têm um padrão senoidal, vamos usar a função senoidal.

A forma geral da função senoidal é:

$$ y = a \cdot \sin(b(x - c)) + d $$

onde $a$ é a amplitude, $d$ é a altura média, $c$ é a fase e $b$ determina a frequência.

3. Determinação da fase A fase ($c$) é ajustada para garantir que a função comece em 0 no ângulo correto. Como a variação ocorre com a primeira maré alta ao meio-dia, podemos calcular:

Se considerarmos que 6h corresponde ao ângulo de $0$ na função senoidal, ajustamos para:

• Para a primeira maré alta em 6h, a função deve ser ajustada:

$$ c = 6 $$

4. Montagem da função final Substituindo os valores já encontrados na função:

$$ y = 1 \cdot \sin\left(\frac{\pi}{6} (x - 6)\right) + 1,7 $$

5. Simplificação e escolha da resposta A fórmula resultante se encaixa na expressão desejada. Simplificando, podemos observar que a altura se mantém entre 0,7 m e 2,7 m.