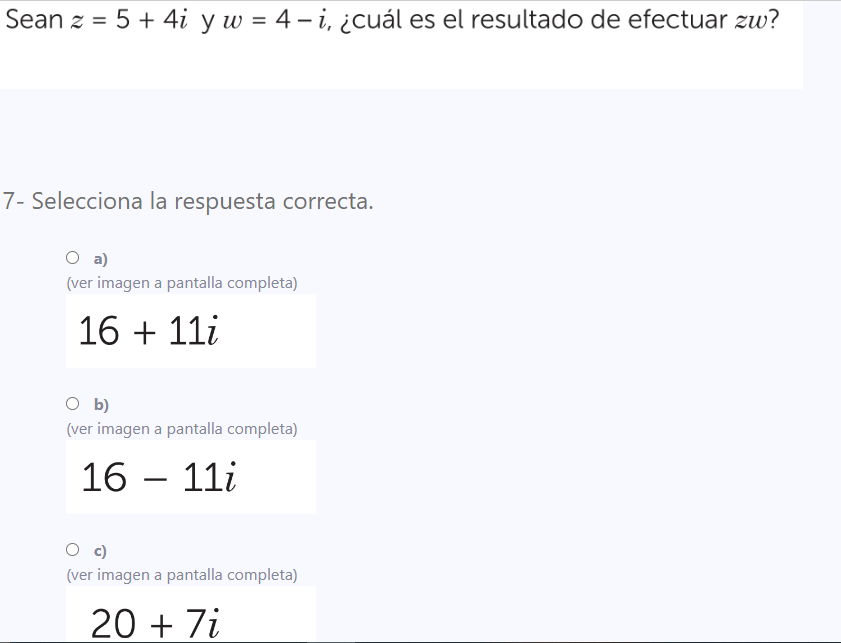
Sean z = 5 + 4i y w = 4 - i, ¿cuál es el resultado de efectuar zw?
Understand the Problem
La pregunta está pidiendo el resultado de multiplicar los números complejos z y w, donde z = 5 + 4i y w = 4 - i. Debemos calcular zu para encontrar el resultado correcto entre las opciones proporcionadas.
Answer
El resultado de \( zw \) es \( 24 + 11i \).
Answer for screen readers
El resultado de multiplicar ( z ) y ( w ) es ( 24 + 11i ).
Steps to Solve
-
Escribe los números complejos
Dado ( z = 5 + 4i ) y ( w = 4 - i ), debes multiplicar estos dos números complejos.
-
Utiliza la propiedad distributiva
Multiplica ( z ) por ( w ) usando la propiedad distributiva:
$$ zw = (5 + 4i)(4 - i) = 5 \cdot 4 + 5 \cdot (-i) + 4i \cdot 4 + 4i \cdot (-i) $$
-
Realiza las multiplicaciones
Ahora calcula cada uno de los productos:
- ( 5 \cdot 4 = 20 )
- ( 5 \cdot (-i) = -5i )
- ( 4i \cdot 4 = 16i )
- ( 4i \cdot (-i) = -4i^2 ) (recuerda que ( i^2 = -1 ), por lo que esto se convierte en ( 4 ))
-
Suma todos los términos
Ahora junta todos los términos:
$$ zw = 20 - 5i + 16i + 4 $$
-
Combina los términos semejantes
Combina los términos reales y los términos imaginarios:
$$ zw = (20 + 4) + (-5i + 16i) = 24 + 11i $$
El resultado de multiplicar ( z ) y ( w ) es ( 24 + 11i ).
More Information
La multiplicación de números complejos se basa en la propiedad distributiva. Un número complejo se expresa en la forma ( a + bi ), donde ( a ) y ( b ) son números reales y ( i ) es la unidad imaginaria.
Tips
- No recordar que ( i^2 = -1 ): Muchos olvidan cambiar ( i^2 ) al multiplicar, lo que puede llevar a errores.
- Errores en la suma de términos: Es fácil perderse en los signos. Organiza siempre los términos semejantes.
AI-generated content may contain errors. Please verify critical information