Sean las señales $x[n] = \alpha^{n} (u[n+a] - u[n-b])$ y $h[n] = \frac{28}{7}(u[-n] - u[-n+c])$ con $a=27$, $b=7$, y $c=25$. Si $y[n] = x[n] * h[n]$, ¿en qué casos $y[n] = 0$?
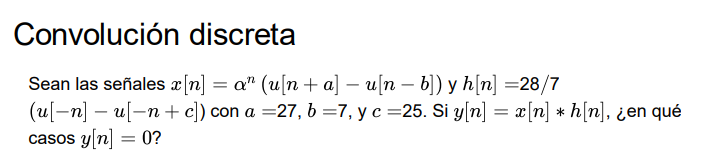
Understand the Problem
La pregunta trata sobre la convolución discreta de dos señales, x[n] y h[n]. Se proporcionan las definiciones de estas señales en términos de funciones escalón unitario (u[n]) y constantes a, b, y c. El objetivo es determinar en qué casos la convolución y[n] = x[n] * h[n] es igual a cero.
Answer
$y[n] = 0$ cuando $n > 5$ o $n < -52$.
Answer for screen readers
$y[n] = 0$ cuando $n > 5$ o $n < -52$.
Steps to Solve
- Simplify $x[n]$ and $h[n]$
First, let's simplify the expressions for $x[n]$ and $h[n]$ using the given values for $a$, $b$, and $c$. We have: $$ x[n] = \alpha^{n} (u[n+27] - u[n-7]) $$ $$ h[n] = \frac{28}{7}(u[-n] - u[-n+25]) = 4(u[-n] - u[-n+25]) $$
- Understand the signals' ranges For the unit step functions to be non-zero, their arguments must be greater than or equal to zero.
For $x[n]$: $u[n+27] = 1$ for $n \geq -27$ and $u[n-7] = 1$ for $n \geq 7$. Therefore, $x[n]$ is non-zero for $-27 \leq n \leq 6$.
For $h[n]$: $u[-n] = 1$ for $-n \geq 0 \implies n \leq 0$ and $u[-n+25] = 1$ for $-n+25 \geq 0 \implies n \leq 25$. Therefore, $h[n]$ is non-zero for $-25 \leq n \leq -1$.
-
Compute the convolution sum The convolution $y[n] = x[n] * h[n]$ is defined as: $$ y[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k] $$
-
Determine the non-zero range for $y[n]$ For $y[n]$ to be non-zero, the ranges of $k$ for which $x[k]$ and $h[n-k]$ are non-zero must overlap. $x[k]$ is non-zero for $-27 \leq k \leq 6$ and $h[n-k]$ is non-zero for $-25 \leq n-k \leq -1$, or equivalently $n+1 \leq k \leq n+25$. Thus we require that $-27 \leq k \leq 6$ and $n+1 \leq k \leq n+25$, so $y[n]$ is only potentially non-zero when the two ranges overlap.
-
Find the range of $n$ where $y[n] = 0$
We want to find when the ranges $-27 \leq k \leq 6$ and $n+1 \leq k \leq n+25$ do not overlap.
- The left end of range 2 is greater than the right end of range 1: $n+1 > 6 \implies n > 5$.
- The right end of range 2 is less than the left end of range 1: $n+25 < -27 \implies n < -52$.
Therefore, $y[n] = 0$ for $n > 5$ and for $n < -52$.
$y[n] = 0$ cuando $n > 5$ o $n < -52$.
More Information
The convolution of two signals results in a new signal that represents the overlapping area of one signal as it is shifted over the other. In this case, when the shift $n$ is such that the non-zero portions of $x[k]$ and $h[n-k]$ do not overlap, the convolution is zero.
Tips
A common mistake is improperly determining the ranges for which $x[n]$ and $h[n]$ (and their shifted/flipped versions) are non-zero. Care must be taken when working with shifted unit step functions. Also, it's easy to make an algebra mistake when determining the range of $n$ for which the signals do not overlap.
AI-generated content may contain errors. Please verify critical information