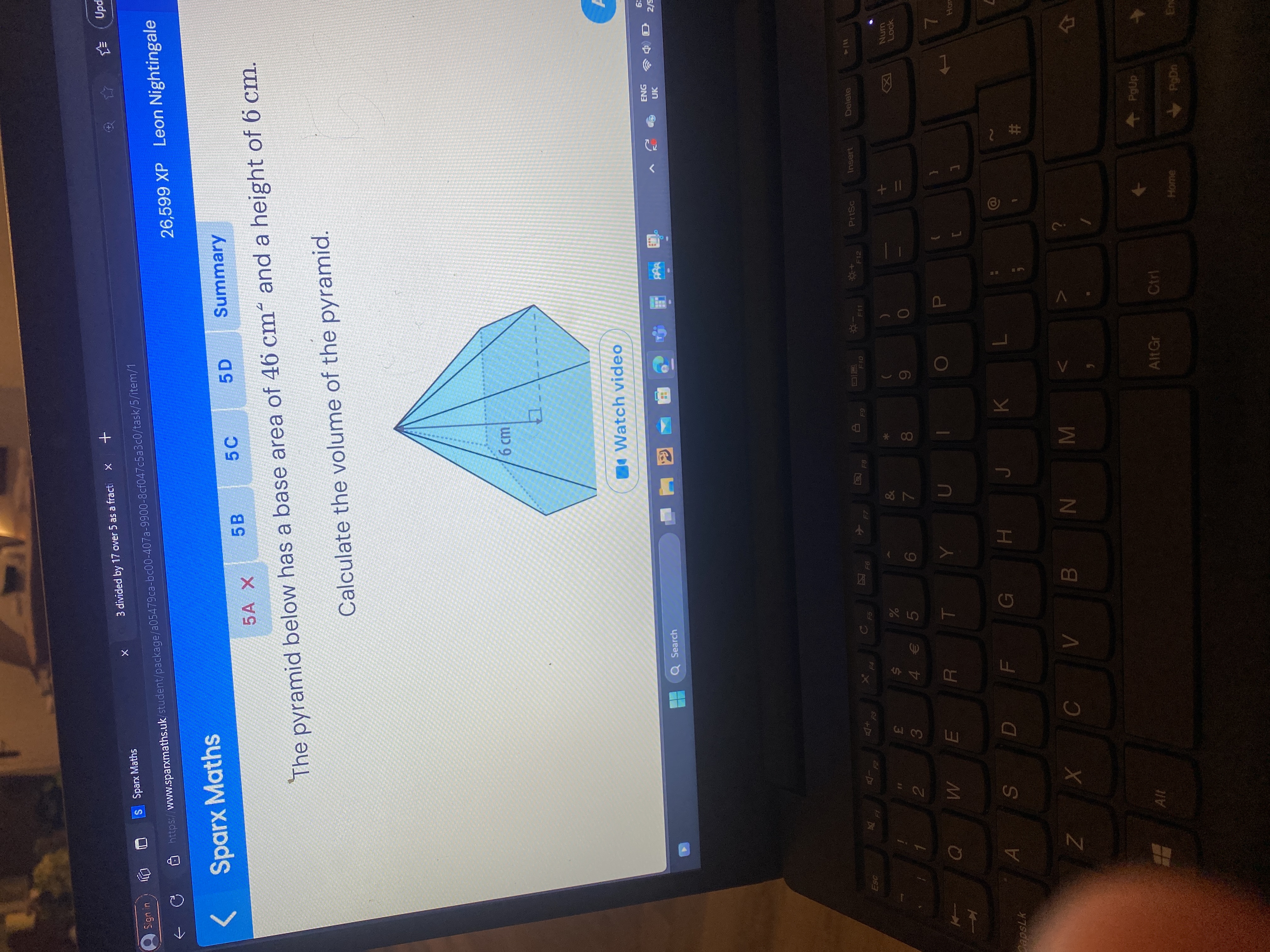
The pyramid below has a base area of 46 cm² and a height of 6 cm. Calculate the volume of the pyramid.
Understand the Problem
The question asks to calculate the volume of a pyramid given its base area and height. This involves applying the formula for the volume of a pyramid, which is V = (1/3) * base area * height.
Answer
The volume of the pyramid is $92 \text{ cm}^3$.
Answer for screen readers
The volume of the pyramid is $92 \text{ cm}^3$.
Steps to Solve
- Write down the formula for the volume of a pyramid
The volume $V$ of a pyramid is given by: $$ V = \frac{1}{3} \times \text{base area} \times \text{height} $$
- Identify the given values
The base area is given as 46 cm$^2$ and the height is given as 6 cm.
- Substitute the values into the formula
Substitute the given values into the formula: $$ V = \frac{1}{3} \times 46 \text{ cm}^2 \times 6 \text{ cm} $$
- Calculate the volume
$$ V = \frac{1}{3} \times 46 \times 6 \text{ cm}^3 $$ $$ V = \frac{1}{3} \times 276 \text{ cm}^3 $$ $$ V = 92 \text{ cm}^3 $$
The volume of the pyramid is $92 \text{ cm}^3$.
More Information
The volume of a pyramid is always one-third of the volume of a prism with the same base area and height.
Tips
A common mistake is forgetting to multiply by $\frac{1}{3}$ in the formula for the volume of a pyramid. Another mistake could be mixing up the units or not including the units in the final answer.
AI-generated content may contain errors. Please verify critical information