Say true or false and justify. 10 x 10^11 = 1001 (iv) 3^0 = (1000)^0.
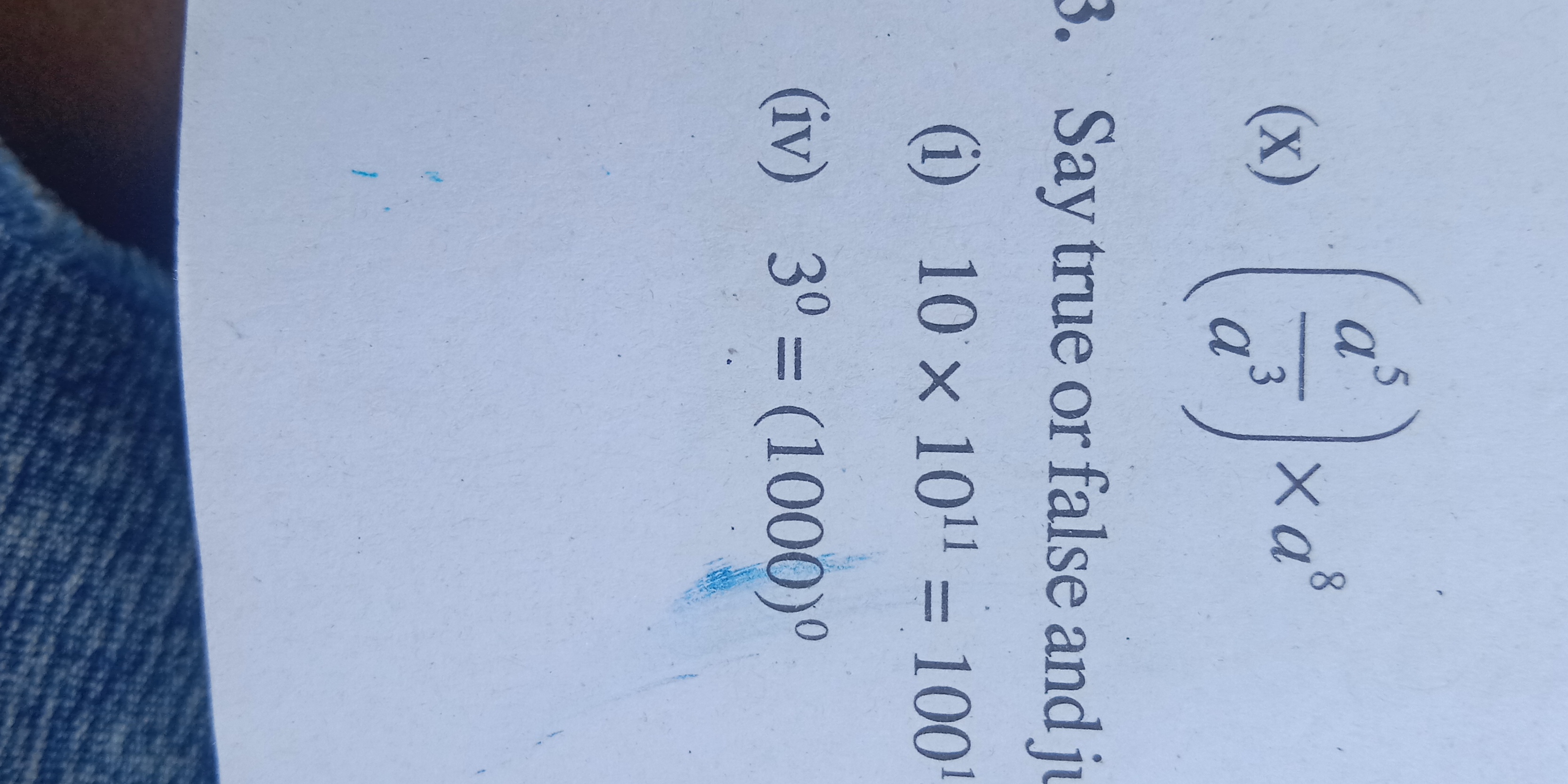
Understand the Problem
The question is asking whether the equation presented is true or false. It involves evaluating expressions with powers and mathematical operations, specifically dealing with exponentiation and multiplication.
Answer
- The first part is **False**. - The second part is **True**.
Answer for screen readers
The answer to the statement is:
-
The first part "$10 \times 10^{11} = 1001$" is False.
-
The second part "$3^0 = (1000)^0$" is True.
Steps to Solve
- Evaluate the first expression: $10 \times 10^{11}$
First, we can use the property of exponents that states $a^m \times a^n = a^{m+n}$.
So:
$$ 10 \times 10^{11} = 10^1 \times 10^{11} = 10^{1+11} = 10^{12} $$
- Determine if $10^{12} = 1001$ is true or false
Now, we compare $10^{12}$ with $1001$.
We know:
$$ 10^{12} = 1,000,000,000,000 $$
Clearly, $10^{12}$ is much larger than $1001$, so the first expression is false.
- Evaluate the second expression: $3^0 = (1000)^0$
Next, we apply the property of exponents that states any non-zero base raised to the power of 0 equals 1.
Thus:
$$ 3^0 = 1 \quad \text{and} \quad (1000)^0 = 1 $$
- Determine if $3^0 = (1000)^0$ is true or false
Since both sides equal 1, we conclude that:
$$ 3^0 = (1000)^0 \quad \Rightarrow \quad \text{True} $$
The answer to the statement is:
-
The first part "$10 \times 10^{11} = 1001$" is False.
-
The second part "$3^0 = (1000)^0$" is True.
More Information
In summary, exponent rules, particularly how powers of zero work and multiplying powers of the same base, are key in solving these expressions. The first expression contrasts significantly in size, while the second reinforces the universal rule for any base other than zero.
Tips
- A common mistake is confusing numbers raised to zero with other values. Always remember that $a^0 = 1$ for any non-zero $a$.
- Miscalculating powers, like thinking $10^{12}$ is similar to smaller numbers instead of realizing its actual value.
AI-generated content may contain errors. Please verify critical information