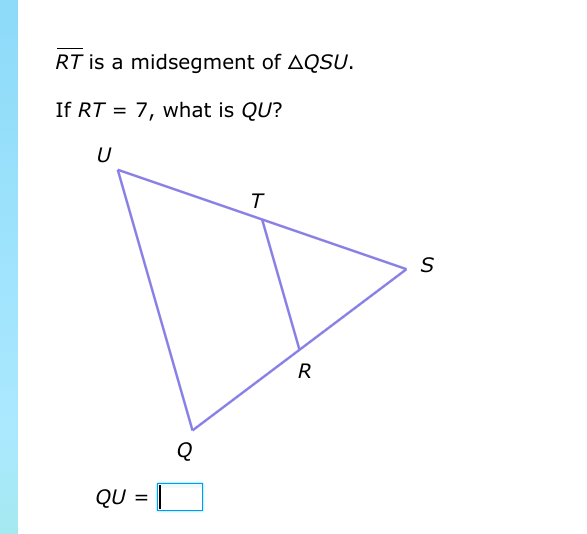
RT is a midsegment of triangle QSU. If RT = 7, what is QU?

Understand the Problem

The question is asking for the length of segment QU in triangle QSU given that RT is a midsegment and that its length is 7. By the properties of a midsegment, it is half the length of the opposite side (QS), allowing us to deduce the length of QU.

Answer

$QU = 14$

Steps to Solve

Understanding the Properties of Midsegments

In a triangle, a midsegment connects the midpoints of two sides. By definition, the length of the midsegment (in this case, $RT$) is half the length of the opposite side ($QS$).

Setting Up the Equation

Since $RT$ is a midsegment and we know its length is 7, we can set up the equation:

$$ RT = \frac{1}{2} QS $$

Substituting the value for $RT$:

$$ 7 = \frac{1}{2} QS $$

Solving for QS

To find $QS$, we'll multiply both sides of the equation by 2:

$$ QS = 2 \times 7 $$

Calculating gives:

$$ QS = 14 $$

Using the Length of QS to Find QU

In triangle $QSU$, segment $QU$ is a side that corresponds to the whole side $QS$. Thus, we can conclude that:

$$ QU = QS = 14 $$

$QU = 14$

More Information

The property of midsegments is useful in various geometry problems, as it allows for simpler calculations of triangle dimensions. Knowing that midsegments are half the length of the opposite side can help solve many related problems.

Tips

A common mistake is confusing the midsegment with other segments in the triangle. Ensure that you correctly identify which segment is the midsegment and which side it corresponds to.
Another mistake is forgetting to multiply by 2 to find the length of the opposite side, which is crucial in using the midsegment property.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!