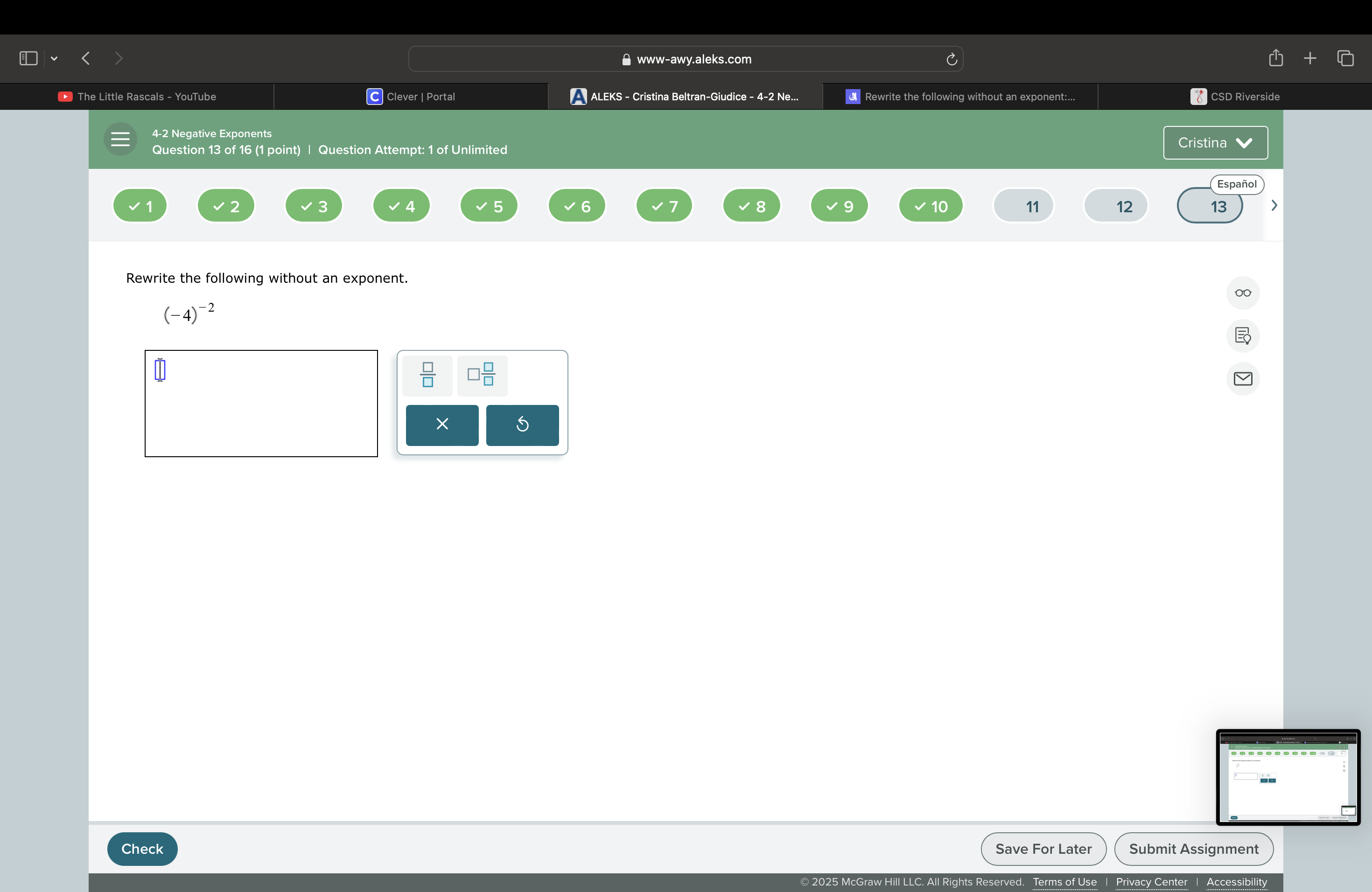
Rewrite the following without an exponent: (-4)^{-2}.
Understand the Problem
The question is asking to rewrite the expression (-4)^{-2} without using an exponent. This involves applying the rules for negative exponents.
Answer
The expression without an exponent is $\frac{1}{16}$.
Answer for screen readers
The expression rewritten without using an exponent is $\frac{1}{16}$.
Steps to Solve
- Understanding Negative Exponent Rule
Using the rule for negative exponents: $$ a^{-n} = \frac{1}{a^{n}} $$
For the expression $(-4)^{-2}$, we rewrite it as: $$ (-4)^{-2} = \frac{1}{(-4)^{2}} $$
- Calculating the Square of -4
Now, calculate $(-4)^{2}$: $$ (-4)^{2} = (-4) \times (-4) = 16 $$
- Final Rewrite of the Expression
Substituting back into our fraction gives: $$ (-4)^{-2} = \frac{1}{16} $$
The expression rewritten without using an exponent is $\frac{1}{16}$.
More Information
By rewriting expressions with negative exponents, you're applying the reciprocal rule, which is a fundamental concept in algebra. In this case, squaring negative numbers yields positive results, reinforcing that multiplying two negatives results in a positive.
Tips
- Confusing negative exponents with negative numbers; remember that a negative exponent simply indicates that you are taking the reciprocal.
- Forgetting to square the base when converting to a positive exponent.
AI-generated content may contain errors. Please verify critical information