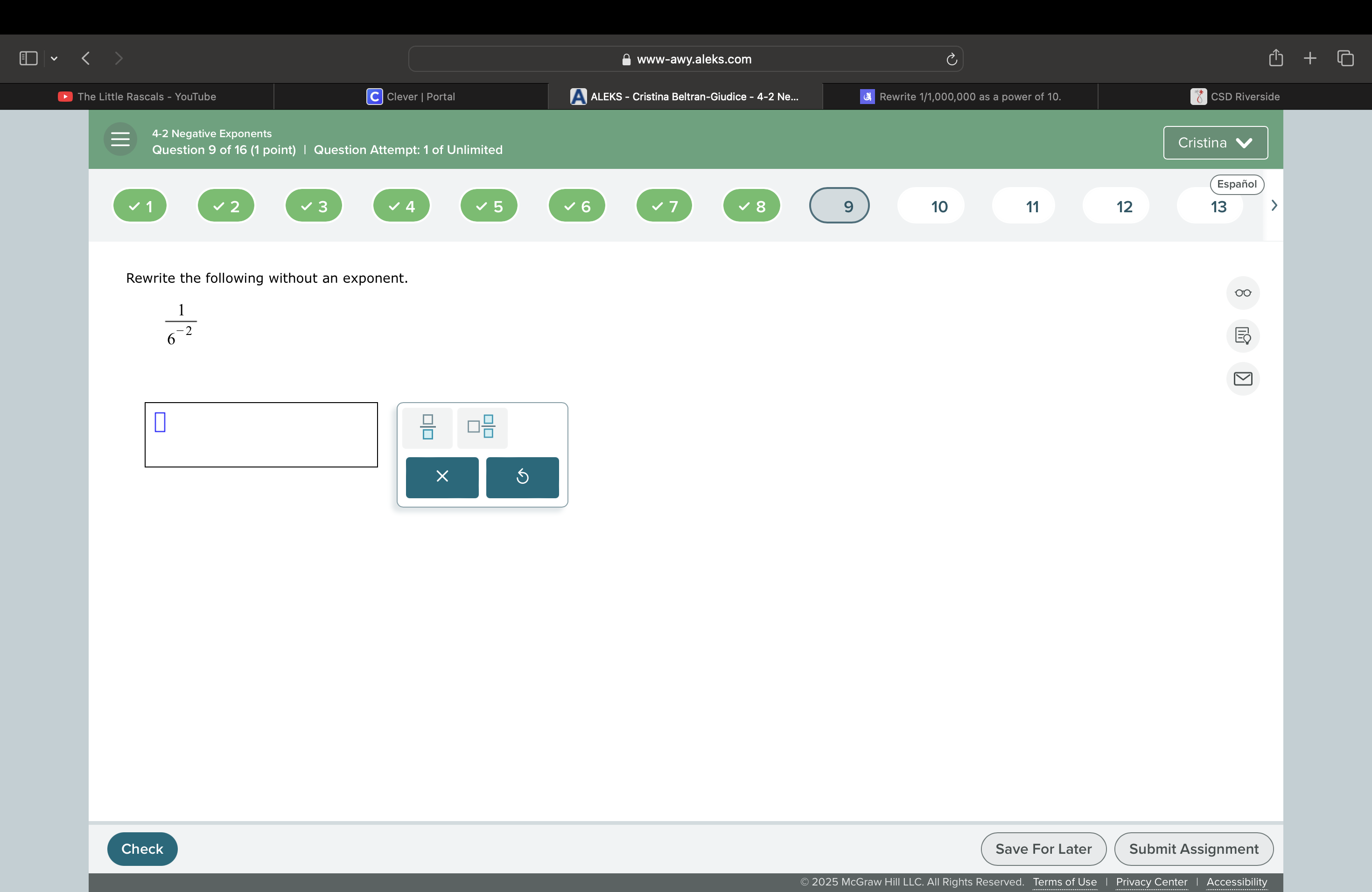
Rewrite the following without an exponent: 1 / 6^(-2)
Understand the Problem
The question asks to rewrite the expression 1/(6^(-2)) without using an exponent. This involves applying the rules of negative exponents.
Answer
36
Answer for screen readers
The expression rewritten without an exponent is 36.
Steps to Solve
-
Rewrite the Exponent To rewrite the expression $1/(6^{-2})$, we first remember that $a^{-n} = \frac{1}{a^n}$. So we can rewrite $6^{-2}$ as $\frac{1}{6^2}$.
-
Substitute into the Expression Now we can substitute this into our original expression: $$ \frac{1}{6^{-2}} = \frac{1}{\frac{1}{6^2}} $$
-
Simplify the Expression When you have a fraction like $\frac{1}{\frac{1}{a}}$, it simplifies to $a$. Therefore, we can simplify: $$ \frac{1}{\frac{1}{6^2}} = 6^2 $$
-
Calculate the Final Answer Now calculate $6^2$: $$ 6^2 = 36 $$
The expression rewritten without an exponent is 36.
More Information
This process utilizes the rules of exponents, particularly how negative exponents indicate reciprocal values. In this case, knowing that a negative exponent signifies turning the base into its reciprocal helped simplify the expression effectively.
Tips
- Confusing the negative exponent with a minus sign: Remember that a negative exponent means "reciprocal", not "negative."
- Forgetting to simplify at the end: Always perform calculations at the final step to ensure accuracy.
AI-generated content may contain errors. Please verify critical information